10.下列图形中,是中心对称图形,但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
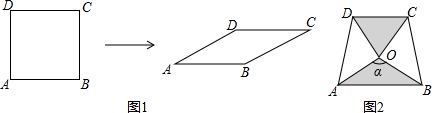
7.如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.
(1)请补全表:
(2)填空:
由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=$\frac{1}{2}$;当α=135°时,S=S(135°)=$\frac{{\sqrt{2}}}{2}$.由上表可以得到S(60°)=S(120°);S(150°)=S(30°),…,由此可以归纳出S(180°-α)=(α°).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).

(1)请补全表:
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{{\sqrt{2}}}{2}$ |
由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=$\frac{1}{2}$;当α=135°时,S=S(135°)=$\frac{{\sqrt{2}}}{2}$.由上表可以得到S(60°)=S(120°);S(150°)=S(30°),…,由此可以归纳出S(180°-α)=(α°).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
4.世界上大部分国家都使用摄氏温度(℃),但美国、英国等国家的天气预报使用华氏温度(℉).两种计量之间有如表对应:
已知华氏温度y(℉)是摄氏温度x(℃)的一次函数.
(1)求该一次函数的表达式;
(2)当华氏温度-4℉时,求其所对应的摄氏温度.
| 摄氏温度x(℃) | … | 0 | 5 | 10 | 15 | 20 | 25 | … |
| 华氏温度y(℉) | … | 32 | 41 | 50 | 59 | 68 | 77 | … |
(1)求该一次函数的表达式;
(2)当华氏温度-4℉时,求其所对应的摄氏温度.
1.在一个不透明的盒子里装有黑、白两种颜色的球共40只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)若从盒子里随机摸出一只球,则摸到白球的概率的估计值为0.6;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
0 285029 285037 285043 285047 285053 285055 285059 285065 285067 285073 285079 285083 285085 285089 285095 285097 285103 285107 285109 285113 285115 285119 285121 285123 285124 285125 285127 285128 285129 285131 285133 285137 285139 285143 285145 285149 285155 285157 285163 285167 285169 285173 285179 285185 285187 285193 285197 285199 285205 285209 285215 285223 366461
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)若从盒子里随机摸出一只球,则摸到白球的概率的估计值为0.6;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
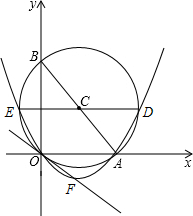 在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}$).
在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}$).
 如图,直线y=kx+b(k≠0)与x轴交于点(-4,0),则关于x的方程kx+b=0的解为x=-4.
如图,直线y=kx+b(k≠0)与x轴交于点(-4,0),则关于x的方程kx+b=0的解为x=-4.