3.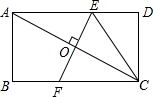 如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
 如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )| A. | 3 | B. | 3.5 | C. | 2.5 | D. | 2.8 |
2.如图a是长方形纸带,∠DEF=21°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
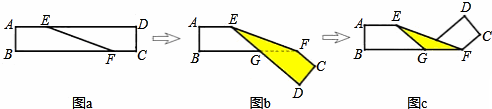

| A. | 117° | B. | 119° | C. | 138° | D. | 159° |
1. 如图,下列条件中,能判定DE∥AC的是( )
如图,下列条件中,能判定DE∥AC的是( )
 如图,下列条件中,能判定DE∥AC的是( )
如图,下列条件中,能判定DE∥AC的是( )| A. | ∠BED=∠EFC | B. | ∠1=∠2 | C. | ∠BEF+∠B=180° | D. | ∠3=∠4 |
19. 六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
(1)其中一次函数是①,②,二次函数是③,④,则⑤,⑥的函数可以定义为三次函数;
(2)我们可以借鉴以前研究函数的经验,先探索函数y=x3的图象和性质;
①填写下表,画出函数的图象;
②观察图象,写出该函数两条不同类型的性质;
(3)若点A(a,b)(a>0)是函数y=x3图象上一点,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C,若顺次连接A,B,C,则△ABC的形状为直角三角形;
(4)函数y=-x3+1的图象关于点(0,1)成中心对称图形.
 六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.(1)其中一次函数是①,②,二次函数是③,④,则⑤,⑥的函数可以定义为三次函数;
(2)我们可以借鉴以前研究函数的经验,先探索函数y=x3的图象和性质;
①填写下表,画出函数的图象;
②观察图象,写出该函数两条不同类型的性质;
| x | … | -2 | -$\frac{3}{2}$ | -1 | 0 | 1 | $\frac{3}{2}$ | 2 | … |
| y=x3 | … | … |
(4)函数y=-x3+1的图象关于点(0,1)成中心对称图形.
17.下列三个命题:①平行四边形既是轴对称图形,又是中心对称图形;②平分弦的直径垂直于这条弦;
③相等圆心角所对的弧相等;④平分弧的直径垂直平分弧所对的弦.其中真命题是( )
③相等圆心角所对的弧相等;④平分弧的直径垂直平分弧所对的弦.其中真命题是( )
| A. | ①④ | B. | ④ | C. | ①② | D. | ②③ |
14.能够判定一个四边形是菱形的条件是( )
0 284689 284697 284703 284707 284713 284715 284719 284725 284727 284733 284739 284743 284745 284749 284755 284757 284763 284767 284769 284773 284775 284779 284781 284783 284784 284785 284787 284788 284789 284791 284793 284797 284799 284803 284805 284809 284815 284817 284823 284827 284829 284833 284839 284845 284847 284853 284857 284859 284865 284869 284875 284883 366461
| A. | 对角线互相垂直平分 | B. | 对角线互相平分且相等 | ||
| C. | 对角线相等且互相垂直 | D. | 对角线互相垂直 |
 某教学学习小组对“人们了解国家大事的途径”进行调查.
某教学学习小组对“人们了解国家大事的途径”进行调查.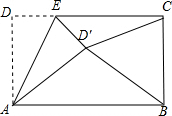 如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中:
如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中: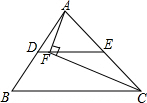 如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,且DF=1,连接AF,CF,若∠AFC=90°,则BC的长度为( )
如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,且DF=1,连接AF,CF,若∠AFC=90°,则BC的长度为( )