2.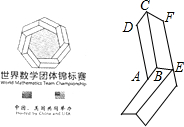 第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )
第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )
 第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )
第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )| A. | 7(a+b+c-d) | B. | 7(a+b-c+d) | C. | 7(a-b+c+d) | D. | 7(b+c+d-a) |
20.如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的横坐标为( )


| A. | 8065 | B. | 8064 | C. | 8063 | D. | 8062 |
19.化简$\frac{16-{a}^{2}}{{a}^{2}+4a+4}$÷$\frac{a-4}{2a+4}$•$\frac{a-2}{a+4}$,其结果是( )
| A. | -2 | B. | 2 | C. | -$\frac{2(a-2)}{a+2}$ | D. | $\frac{2}{(a+2)^{2}}$ |
17.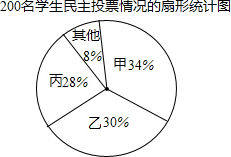 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:| 试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
16.某校举办初中生演讲比赛,每班派一名学生参赛,现某班有A,B,C三名学生竞选,他们的笔试成绩和口试成绩分别用两种方式进行了统计,如表和图1:

(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本年级段的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按3:4:3的比例确定最后成绩,请计算这三名学生的最后成绩,并根据最后成绩判断谁能当选.
0 284681 284689 284695 284699 284705 284707 284711 284717 284719 284725 284731 284735 284737 284741 284747 284749 284755 284759 284761 284765 284767 284771 284773 284775 284776 284777 284779 284780 284781 284783 284785 284789 284791 284795 284797 284801 284807 284809 284815 284819 284821 284825 284831 284837 284839 284845 284849 284851 284857 284861 284867 284875 366461
| 学生 | A | B | C |
| 笔试成绩(单位:分) | 85 | 95 | 90 |
| 口试成绩(单位:分) | 90 | 80 | 85 |

(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本年级段的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按3:4:3的比例确定最后成绩,请计算这三名学生的最后成绩,并根据最后成绩判断谁能当选.
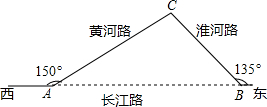 如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)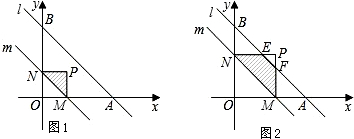
 阅读下列材料:
阅读下列材料: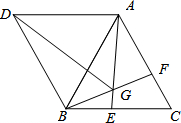 如图,平行四边形ADBC中,∠C=60°,AC=BC,点E、F分别在BC、AC上,BE=CF,AE=BF交于点G.
如图,平行四边形ADBC中,∠C=60°,AC=BC,点E、F分别在BC、AC上,BE=CF,AE=BF交于点G.


