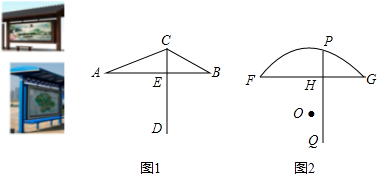
19.小红、小明在玩“剪子、包袱、锤子”游戏,小红给自己一个规定:一直不出“锤子”.小红、小明获胜的概率分别是P1,P2,则下列结论正确的是( )
| A. | P1=P2 | B. | P1>P2 | C. | P1<P2 | D. | P1≤P2 |
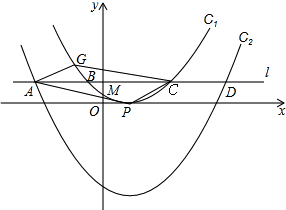
17. 已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )
已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )
 已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )
已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )| A. | (5,8) | B. | (5,10) | C. | (4,8) | D. | (3,10) |
15. 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )
如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )
 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )
如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )| A. | 24 | B. | 12 | C. | 6 | D. | 8 |
14.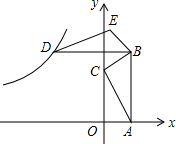 如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y=$\frac{k}{x}$图象恰好过点D,则k的值为( )
如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y=$\frac{k}{x}$图象恰好过点D,则k的值为( )
 如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y=$\frac{k}{x}$图象恰好过点D,则k的值为( )
如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y=$\frac{k}{x}$图象恰好过点D,则k的值为( )| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
12.某书店准备购进甲、乙两种图书共100本,购书款不高于2224元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的函数知识来解决)
0 284405 284413 284419 284423 284429 284431 284435 284441 284443 284449 284455 284459 284461 284465 284471 284473 284479 284483 284485 284489 284491 284495 284497 284499 284500 284501 284503 284504 284505 284507 284509 284513 284515 284519 284521 284525 284531 284533 284539 284543 284545 284549 284555 284561 284563 284569 284573 284575 284581 284585 284591 284599 366461
| 甲种图书 | 乙种图书 | |
| 进价(元/本) | 16 | 28 |
| 售价(元/本) | 26 | 40 |
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的函数知识来解决)