11.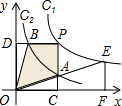 如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )
如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )
 如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )
如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )| A. | $\sqrt{3}$﹕1 | B. | 2﹕$\sqrt{3}$ | C. | 2﹕1 | D. | 29﹕14 |
9.表中给出了变量x与ax2、ax2+bx+c之间的部分对应关系(表格中的符号“--”表示该项数据已经丢失):
(1)求函数y=ax2+bx+c的表达式;
(2)将函数y=ax2+bx+c的图象向左平移1个单位长度,再向上平移2个单位长度,直接写出平移后图象的表达式.
| x | -1 | 0 | 1 |
| ax2 | -- | -- | 1 |
| ax2+bx+c | 7 | 2 | -- |
(2)将函数y=ax2+bx+c的图象向左平移1个单位长度,再向上平移2个单位长度,直接写出平移后图象的表达式.
6.甲、乙两地5月下旬的日平均气温统计如表(单位:℃):
则甲、乙两地这10天日平均气温的方差大小关系为:S甲2>S乙2.(填“>”、“<”或“=”)
| 甲地气温 | 24 | 30 | 28 | 24 | 22 | 26 | 27 | 26 | 29 | 24 |
| 乙地气温 | 24 | 26 | 25 | 26 | 24 | 27 | 28 | 26 | 28 | 26 |
4.记n边形(n>3)的一个外角的度数为p,与该外角不相邻的(n-1)个内角的度数的和为q,则p与q的关系是( )
| A. | p=q | B. | p=q-(n-1)•180° | C. | p=q-(n-2)•180° | D. | p=q-(n-3)•180° |
3.秦淮区将开展南部新城规划建设,在包括近10平方公里核心区及其外围的整个南部新城投入150 000 000 000元,10年后将其打造成南京“第二个河西”.将150 000 000 000用科学记数法表示为( )
0 283271 283279 283285 283289 283295 283297 283301 283307 283309 283315 283321 283325 283327 283331 283337 283339 283345 283349 283351 283355 283357 283361 283363 283365 283366 283367 283369 283370 283371 283373 283375 283379 283381 283385 283387 283391 283397 283399 283405 283409 283411 283415 283421 283427 283429 283435 283439 283441 283447 283451 283457 283465 366461
| A. | 0.15×1012 | B. | 1.5×1011 | C. | 1.5×1012 | D. | 1.5×1013 |
 如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.
如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F. 如图,在△ABC中,BC的垂直平分线交它的外接圆于D、E两点.若∠B=24°,∠C=106°,则$\widehat{AD}$的度数为82°.
如图,在△ABC中,BC的垂直平分线交它的外接圆于D、E两点.若∠B=24°,∠C=106°,则$\widehat{AD}$的度数为82°.