题目内容
①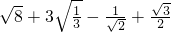 ;
;
② ;
;
③3(x-2)2=x(x-2);
④ .
.
解:① +3
+3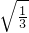 -
- +
+
=2 +
+ -
- +
+
= +
+ .
.
②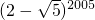
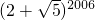
=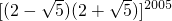 •(2+
•(2+ )
)
=(4-5)2005•(2+ )
)
=-(2+ )
)
=-2- .
.
③3(x-2)2=x(x-2)
3(x-2)2-x(x-2)=0
(x-2)[3(x-2)-x]=0
(x-2)(2x-6)=0
∴x-2=0或2x-6=0
∴x1=2,x2=3.
④
3x2-2x-1=0
(3x+1)(x-1)=0
3x+1=0或x-1=0
∴x1=- ,x2=1.
,x2=1.
分析:①先把各个式子化成最简二次根式,再合并同类项;
②运用平方差公式和积的乘方法则进行计算;
③把右边的项移到左边,用因式分解法解方程;
④把方程化成3x2-2x-1=0,得(3x+1)(x-1)=0可以求出方程的两个根.
点评:①考查的是二次根式的计算,把每个二次根式化成最简二次根式,然后合并;②考查的是积的乘方法则,运用法则进行计算;③考查的是用因式分解法解一元二次方程,根据题目特点用提公因式法因式分解,求出方程的两个根;④考查的是用因式分解法解方程,根据题目特点,用分组分解法因式分解,求出方程的两个根.
 +3
+3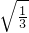 -
- +
+
=2
 +
+ -
- +
+
=
 +
+ .
.②
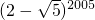
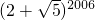
=
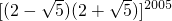 •(2+
•(2+ )
)=(4-5)2005•(2+
 )
)=-(2+
 )
)=-2-
 .
.③3(x-2)2=x(x-2)
3(x-2)2-x(x-2)=0
(x-2)[3(x-2)-x]=0
(x-2)(2x-6)=0
∴x-2=0或2x-6=0
∴x1=2,x2=3.
④

3x2-2x-1=0
(3x+1)(x-1)=0
3x+1=0或x-1=0
∴x1=-
 ,x2=1.
,x2=1.分析:①先把各个式子化成最简二次根式,再合并同类项;
②运用平方差公式和积的乘方法则进行计算;
③把右边的项移到左边,用因式分解法解方程;
④把方程化成3x2-2x-1=0,得(3x+1)(x-1)=0可以求出方程的两个根.
点评:①考查的是二次根式的计算,把每个二次根式化成最简二次根式,然后合并;②考查的是积的乘方法则,运用法则进行计算;③考查的是用因式分解法解一元二次方程,根据题目特点用提公因式法因式分解,求出方程的两个根;④考查的是用因式分解法解方程,根据题目特点,用分组分解法因式分解,求出方程的两个根.

练习册系列答案
相关题目
 ,其中
,其中 .
. ;
; ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来. 如图,AB∥CD,则下列等式成立的是
如图,AB∥CD,则下列等式成立的是