题目内容
8.若二次函数y=x2-mx的对称轴是x=2,则关于x的方程x2-mx=5的解为( )| A. | x1=1,x2=5 | B. | x1=1,x2=3 | C. | x1=1,x2=-5 | D. | x1=-1,x2=5 |
分析 先根据二次函数y=x2+mx的对称轴是x=2求出m的值,再把m的值代入方程x2+mx=5,求出x的值即可.
解答 解:∵二次函数y=x2+mx的对称轴是x=2,
∴-$\frac{m}{2}$=2,
解得m=-4,
∴关于x的方程x2+mx=5可化为x2-4x-5=0,即(x+1)(x-5)=0,解得x1=-1,x2=5.
故选D.
点评 本题考查的是二次函数的性质,熟知二次函数的对称轴方程是解答此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
3.下列命题为真命题的是( )
| A. | 若a2=b2,则a=b | |
| B. | 等角的补角相等 | |
| C. | b边形的外角和为(n-2)=180° | |
| D. | 若$\overline{{x}_{乙}}$=$\overline{{x}_{甲}}$,S${\;}_{甲}^{2}$>S${\;}_{乙}^{2}$,则甲数据更稳定 |
13.若x=-3可以使一个二次根式有意义,这个二次根式可以是( )
| A. | $\sqrt{1+x}$ | B. | $\sqrt{2x+5}$ | C. | $\sqrt{3x-4}$ | D. | $\sqrt{4-x}$ |
20. 在四边形ABCD中,如果∠A+∠B+∠C=260°,那么∠D的度数为( )
在四边形ABCD中,如果∠A+∠B+∠C=260°,那么∠D的度数为( )
 在四边形ABCD中,如果∠A+∠B+∠C=260°,那么∠D的度数为( )
在四边形ABCD中,如果∠A+∠B+∠C=260°,那么∠D的度数为( )| A. | 120° | B. | 110° | C. | 100° | D. | 90° |
17.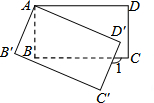 如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,若旋转角为20°,则∠1为( )
如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,若旋转角为20°,则∠1为( )
 如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,若旋转角为20°,则∠1为( )
如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,若旋转角为20°,则∠1为( )| A. | 110° | B. | 120° | C. | 150° | D. | 160° |
18.下列图标中,是轴对称的是( )
| A. |  | B. |  | C. |  | D. |  |