题目内容
2．
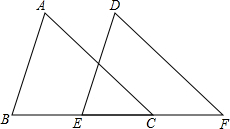如图，点B、E、C、F在同一条直线上，∠A=∠D，∠B=∠DEF，BE=CF．求证：AB=DE．
分析 先证明BC=EF，然后依据AAS证明△ABC≌△DEF，最后依据全等三角形的性质进行证明即可．
解答 证明：∵BE=CF，
∴BE+EC=CF+EC，即BC=EF．
在△ABC和△DEF中$\left\{\begin{array}{l}{∠A=∠D}\\{∠B=∠DEF}\\{BC=EF}\end{array}\right.$，
∴△ABC≌△DEF．
∴AB=DE．
点评 本题主要考查的是全等三角形的判定与性质，熟练掌握全等三角形的性质和判定定理是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12．
如图，△ABC和△EFC都是等边三角形，AD是△ABC的高，AB=4，若点E在直线AD上运动，连接DF，则在点E运动过程中，线段DF的最小值是（ ）
如图，△ABC和△EFC都是等边三角形，AD是△ABC的高，AB=4，若点E在直线AD上运动，连接DF，则在点E运动过程中，线段DF的最小值是（ ）| A． | 1 | B． | 2 | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
10．△ABC中，∠A=25°，∠B=87°，则∠C=（ ）
| A． | 58° | B． | 68° | C． | 78° | D． | 87° |
7．
如图，在Rt△ABC中，∠B=90°，AB=3，AC=5，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点B′处，则BE的长为（ ）
如图，在Rt△ABC中，∠B=90°，AB=3，AC=5，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点B′处，则BE的长为（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{3}{2}$ | D． | 2 |
11．下列四个方程中，是一元一次方程的是（ ）
| A． | 2x-y=1 | B． | x 2-3 x+1=0 | C． | x=7 | D． | $\frac{2}{x}$=1 |
