题目内容
【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( )
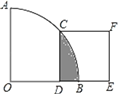
A. 2π﹣8 B. 4π﹣8 C. 2π﹣4 D. 4π﹣4
【答案】C
【解析】试题分析:连接OC,根据C是弧AB的中点,∠AOB=90°,可知∠COB=45°,则有△ODC是等腰直角三角形,再根据勾股定理可求得OC=4;然后根据扇形面积的计算公式可求出S扇形OCB,根据三角形面积的计算公式可求出S△ODC,再根据S阴影=S扇形OCB-S△ODC可求出阴影部分的面积.
解:如图所示,连接OC:

∵C是弧AB的中点,∠AOB=90°,
∴∠COB=45°.
∵四边形CDEF是正方形,且其边长为2![]() ,
,
∴∠ODC=90°,CD=2![]() ,
,
∴在Rt△ODC中,OD=CD=2![]() ,OC=
,OC=![]() =4,
=4,
∴S扇形OCB=![]() ·π·42=2π,S△ODC=
·π·42=2π,S△ODC=![]() OD·CD=4,
OD·CD=4,
∴S阴影=S扇形OCB-S△ODC=2π-4.
故选C.

练习册系列答案
相关题目