题目内容
直角三角形边长为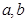 ,斜边上高为
,斜边上高为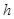 ,则下列各式总能成立的是( )
,则下列各式总能成立的是( )
A. 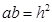 B.
B.
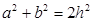
C. 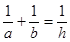 D.
D. 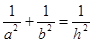
【答案】
D
【解析】
试题分析:根据直角三角形的面积公式,再结合勾股定理即可判断.
根据直角三角形的面积可得 ,则
,则 ,
,
根据勾股定理可得 ,
,
则可得 ,即
,即 ,
,
两边同除以 得
得 ,
,
故选D.
考点:本题考查的是直角三角形的面积公式,勾股定理
点评:解答本题的关键是熟练运用勾股定理、直角三角形的面积公式以及等式的性质进行变形.

练习册系列答案
相关题目
如图所示,在4×4的菱形斜网格图中(每一个小菱形的边长为1,有一个角是60°),菱形ABCD的边长为2,E是AD的中点,按CE将菱形ABCD剪成①、②两部分,用这两部分可以分别拼成直角三角形、等腰梯形、矩形,要求所拼成图形的顶点均落在格点上.
1.(1)在下面的菱形斜网格中画出示意图;
 |
2.
|
|
面积关系是 ;
周长关系是 .
如图所示,在4×4的菱形斜网格图中(每一个小菱形的边长为1,有一个角是60°),菱形ABCD的边长为2,E是AD的中点,按CE将菱形ABCD剪成①、②两部分,用这两部分可以分别拼成直角三角形、等腰梯形、矩形,要求所拼成图形的顶点均落在格点上.
1.(1)在下面的菱形斜网格中画出示意图;
 |
2.
|
|
 )、周长(
)、周长( )的大小关系(用“=”、“>”或“<”连接):
)的大小关系(用“=”、“>”或“<”连接):
面积关系是 ;
周长关系是 .