题目内容
13.点E在正方形ABCD的边BC上,点F在AE上,连接FB,FD,∠ABF=∠AFB.(1)如图1,求证:∠AFD=∠ADF;
(2)如图2,过点F作垂线交AB于G,交DC的延长线于H,求证:DH=2AG;
(3)在(2)的条件下,若EF=2,CH=3,求EC的长.

分析 (1)利用等腰三角形的性质结合正方形的性质得出AF=AD,则∠AFD=∠ADF;
(2)首先得出四边形AGHN为平行四边形,得出FM=MD,进而NF=NH,ND=NH,即可得出答案;
(3)首先得出△ADN≌△DCP(ASA),进而PC=DN,再利用在Rt△ABE中,BE2+AB2=AE2,求出答案.
解答 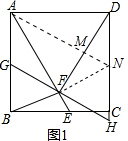 (1)证明:∵∠ABF=∠AFB,
(1)证明:∵∠ABF=∠AFB,
∴AB=AF,
∵四边形ABCD为正方形,
∴AB=AD,
∴AF=AD,
∴∠AFD=∠ADF;
(2)证明:如图1所示:过点A作DF的垂线分别交DF,DH于M,N两点
∵GF⊥DF,
∴∠GFD=∠AMD=90°,
∴AN∥GH,
∵四边形ABCD为正方形,
∴AG∥NH,
∴四边形AGHN为平行四边形,
∴AG=NH,
∵AF=AD,AM⊥FD,
∴FM=MD,
连接NF,则NF=ND,
∴∠NFD=∠NDF,
∵∠NFD+∠NFH=∠NDF+∠H,
∴∠NFH=∠H,
∴NF=NH,
∴ND=NH,
∴DH=2NH=2AG;
(3)解:延长DF交BC于点P,如图2所示:
∵四边形ABCD为正方形,
∴AD∥BC,
∴∠ADF=∠FPE,
∴∠PFE=∠AFD=∠ADF=∠FPE,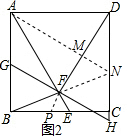
∴EF=EP=2,
∵∠DAM+∠ADM=∠ADM+∠PDC,
∴∠DAM=∠PDC,
∵四边形ABCD为正方形,
∴AD=DC,∠ADN=∠DCP,
在△ADN和△DCP中
$\left\{\begin{array}{l}{∠DAN=∠PDC}\\{AD=DC}\\{∠ADN=∠PCD}\end{array}\right.$,
∴△ADN≌△DCP(ASA),
∴PC=DN,
设EC=x,则PC=DN=x+2,DH=2x+4,
∵CH=3,
∴DC=AB=BC=AF=2x+1
∴AE=2x+3,BE=x+1,
在Rt△ABE中,BE2+AB2=AE2,
∴(x+1)2+(2x+1)2=(2x+3)2.
整理得:x2-6x-7=0,
解得:x1=7,x2=-1(不合题意,舍去)
∴EC=7.
点评 此题主要考查了四边形综合以及全等三角形的判定与性质以及勾股定理和正方形的性质、平行四边形的性质等知识,正确把握正方形的性质是解题关键.

| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C. | $\sqrt{40}$÷$\sqrt{5}$=2$\sqrt{2}$ | D. | $\sqrt{(-15)^{2}}$=-15 |
| A. | y=2x | B. | y=2x-6 | C. | y=4x-3 | D. | y=-x-3 |
| A. | m>4 | B. | m<4 | C. | m>$\frac{4}{3}$ | D. | m<$\frac{4}{3}$ |



