题目内容
已知y=y1+y2,y1与x2成正比例,y2是x的一次函数,当x=2时,y=-1,当x=-1时,y=4,当x=1时,y=3,求y关于x的函数解析式.
考点:待定系数法求二次函数解析式
专题:
分析:根据y1与x2成正比例,y2是x的一次函数,可设y1=ax2,y2=kx+b,又因为y=y1+y2,得到y关于x的函数关系式,再进一步代入x,y的值得到方程组,从而求得函数关系式.
解答:解:根据题意,设y1=ax2,y2=kx+b,
又∵y=y1+y2,
∴y=ax2+kx+b;
又∵x=2时,y=-1,当x=-1时,y=4,当x=1时,y=3,
∴
,
解得
.
∴y关于x的函数解析式为:y=-
2-
x+
.
又∵y=y1+y2,
∴y=ax2+kx+b;
又∵x=2时,y=-1,当x=-1时,y=4,当x=1时,y=3,
∴
|
解得
|
∴y关于x的函数解析式为:y=-
| 7 |
| 6 |
| 1 |
| 2 |
| 14 |
| 3 |
点评:考查了待定系数法求一次函数解析式,此题首先根据题意分别建立y1与x,y2与x的函数关系式,再进一步得到y与x之间的函数关系式,然后代入得到关于a、k、的方程组,从而求解.

练习册系列答案
相关题目
有下列四个命题:
①对顶角相等;
②内错角相等;
③有两边和其中一边的对角对应相等的两个三角形全等;
④在同一平面内,如果两条直线都垂直于第三条直线,那么这两条直线平行.
其中真命题有( )
①对顶角相等;
②内错角相等;
③有两边和其中一边的对角对应相等的两个三角形全等;
④在同一平面内,如果两条直线都垂直于第三条直线,那么这两条直线平行.
其中真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,半圆O的直径AB=10cm,弦AD=3
如图,半圆O的直径AB=10cm,弦AD=3| 10 |
A、4
| ||
| B、8cm | ||
C、2
| ||
| D、6cm |
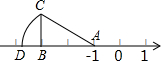 如图,直角三角形ABC的直角边AB在数轴上,点A表示的实数为-1,以A为圆心,AC的长为半径作弧交数轴的负半轴于D,若CB=1,AB=2,则点D表示的实数为( )
如图,直角三角形ABC的直角边AB在数轴上,点A表示的实数为-1,以A为圆心,AC的长为半径作弧交数轴的负半轴于D,若CB=1,AB=2,则点D表示的实数为( )A、
| ||
B、-
| ||
C、-
| ||
D、-
|