题目内容
11.已知|x-1|+(y+3)2=0,则分式$\frac{y-x}{y}$的值是( )| A. | $-\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $-\frac{3}{4}$ |
分析 首先根据非负数的性质可求出x、y的值,进而可求出结果.
解答 解:∵|x-1|+(y+3)2=0,
∴x-1=0,x=1,
y+3=0,y=-3,
∴原式=1-$\frac{x}{y}$=1$+\frac{1}{3}$=$\frac{4}{3}$,
故选A.
点评 本题考查了非负数的性质,利用非负数的性质解得x,y是解答此题的关键.

练习册系列答案
相关题目
3.解方程$\frac{2x-1}{3}$=1-$\frac{x+1}{6}$,通过去分母的变形,得( )
| A. | 2x-1=1-x+1 | B. | 3(2x-1)=1-x+1 | C. | 2(2x-1)=6-(x+1) | D. | 3(2x-1)=6-6(x+1) |
20.下列说法中正确的是( )
| A. | 带根号的数都是无理数 | B. | 实数都是有理数 | ||
| C. | 有理数都是实数 | D. | 无理数都是开方开不尽的数 |
 如图,某河道要建造一座公路桥,要求桥面离地面高度AC为3米,公路桥的坡角∠ABC为30°,则公路桥的水平距离BC的长是3$\sqrt{3}$米.(结果保留根号)
如图,某河道要建造一座公路桥,要求桥面离地面高度AC为3米,公路桥的坡角∠ABC为30°,则公路桥的水平距离BC的长是3$\sqrt{3}$米.(结果保留根号)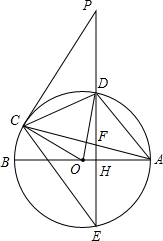 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于点D、E,交AB于点H,交AC于点F,P是延长线上一点,且PC=PF.
如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于点D、E,交AB于点H,交AC于点F,P是延长线上一点,且PC=PF. 北京市在城市建设中,要折除旧烟囱AB,在烟囱正西方向的楼CD的顶端C,测得烟囱的顶端A的仰角为45°,底端B的俯角为30°,已量得DB=21m.拆除时若让烟囱向正东倒下,试问:距离烟囱东方35m远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
北京市在城市建设中,要折除旧烟囱AB,在烟囱正西方向的楼CD的顶端C,测得烟囱的顶端A的仰角为45°,底端B的俯角为30°,已量得DB=21m.拆除时若让烟囱向正东倒下,试问:距离烟囱东方35m远的一棵大树是否被歪倒的烟囱砸着?请说明理由.