题目内容
在⊙O中
的度数为130°，则它所对的圆心角=________，所对的圆周角=________．
130° 65°
分析：根据圆心角的度数等于它所对的弧的度数，得到∠AOB=130°，再根据圆周角定理可得∠APB=
∠AOB=×130°=65°．
解答：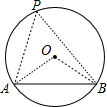
解：如图，∠APB是弧AB所对的圆周角，
∵的度数为130°，
∴∠AOB=130°，
∴∠APB=∠AOB=×130°=65°，
即弧AB的度数为65°．
点评：本题考查了圆周角定理．在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．
分析：根据圆心角的度数等于它所对的弧的度数，得到∠AOB=130°，再根据圆周角定理可得∠APB=
∠AOB=×130°=65°．解答：
解：如图，∠APB是弧AB所对的圆周角，∵
的度数为130°，∴∠AOB=130°，
∴∠APB=
∠AOB=×130°=65°，即弧AB的度数为65°．
点评：本题考查了圆周角定理．在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．
练习册系列答案
阅读快车系列答案
相关题目
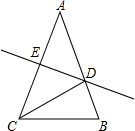如图，在△ABC中，AB=AC，AC的垂直平分线分别交AB、AC于点D、E．