题目内容
⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是
- A.7
- B.17
- C.7或17
- D.34
C
分析:先作出图象根据勾股定理分别求出弦AB、CD的弦心距OE、OF,再根据两弦在圆心同侧和在圆心异侧两种情况讨论.
解答: 解:如图,AE=
解:如图,AE= AB=
AB= ×24=12,
×24=12,
CF= CD=
CD= ×10=5,
×10=5,
OE=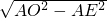 =
= =5,
=5,
OF= =
=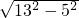 =12,
=12,
①当两弦在圆心同侧时,距离=OF-OE=12-5=7;
②当两弦在圆心异侧时,距离=OE+OF=12+5=17.
所以距离为7或17.
故选C.
点评:先构造半径、弦心距、半弦长为边长的直角三角形,再利用勾股定理求弦心距,本题要注意分两种情况讨论.
分析:先作出图象根据勾股定理分别求出弦AB、CD的弦心距OE、OF,再根据两弦在圆心同侧和在圆心异侧两种情况讨论.
解答:
 解:如图,AE=
解:如图,AE= AB=
AB= ×24=12,
×24=12,CF=
 CD=
CD= ×10=5,
×10=5,OE=
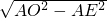 =
= =5,
=5,OF=
 =
=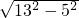 =12,
=12,①当两弦在圆心同侧时,距离=OF-OE=12-5=7;
②当两弦在圆心异侧时,距离=OE+OF=12+5=17.
所以距离为7或17.
故选C.
点评:先构造半径、弦心距、半弦长为边长的直角三角形,再利用勾股定理求弦心距,本题要注意分两种情况讨论.

练习册系列答案
相关题目
⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
| A、7 | B、17 | C、7或17 | D、34 |