题目内容
 已知,如图,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
已知,如图,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
试证明点P在∠AOB的平分线上.
 证明:经过点P作射线OC,
证明:经过点P作射线OC,∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO.
在Rt△PDO和Rt△PEO中,
 ,
,∴Rt△PDO≌Rt△PEO(HL),
∴∠AOC=∠BOC,
∴OC是∠AOB的平分线,即P点在∠AOB的平分线上.
分析:这是角平分线的逆定理,可利用全等三角形证明∠AOC=∠BOC,即OC是∠AOB的平分线,P点在∠AOB的平分线上.
点评:本题主要考查了角平分线的性质定理的逆定理:到角的两边距离相等的点在角的平分线上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图,PD⊥OB,PE⊥OA,垂足分别为D、E,且PD=PE.
已知,如图,PD⊥OB,PE⊥OA,垂足分别为D、E,且PD=PE.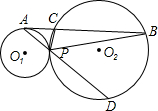 线AP交圆O2于点D,连接DC、PC.
线AP交圆O2于点D,连接DC、PC. 已知,如图在等腰三角形ABC中,AB=AC,P为BC的中点,PD⊥AB于点D,PE⊥AC于点E,求证:PD=PE.
已知,如图在等腰三角形ABC中,AB=AC,P为BC的中点,PD⊥AB于点D,PE⊥AC于点E,求证:PD=PE.