题目内容
2.在平面直角坐标系中,已知点A(1,1)、B(4,1)、C(2,3),若以A、B、C、D为顶点的四边形是平行四边形,则点D的坐标为(-1,3)或(5,3)或(3,-1).分析 在平面直角坐标系中描出A、B、C三个点,分AB为边和AB为对角线分别求出D点坐标,当AB为边时,过C作CD∥AB,且CD=AB,可求得D点坐标,当AB为对角线时,过B作BD∥AC,
解答 解:
①当AB为四边形的边时,过C作CD∥AB,如图1,
∵A(1,1),B(4,1),
∴AB=3,
∵四边形为平行四边形,
∴CD=AB=3,
∵C(2,3),
∴可设D点坐标为(x,3),
∴|x-2|=3,解得x=5或x=-1,
此时D点坐标为(-1,3)或(5,3);
②当AB为四边形的对角线时,过B作BD∥AC,使BD=AC,则D点即为所求,如图2,
又由①可知在AB上方的点即为(5,3),只需求在AB下方的点即可,
过D作DE⊥AB于点E,过C作CF⊥AB于点F 
∵AC∥BC,
∴∠A=∠DBE,
在△ACF和△BDE中
$\left\{\begin{array}{l}{∠A=∠DBE}\\{∠AFC=∠DEB}\\{AC=BD}\end{array}\right.$
∴△ACF≌△BDE(AAS),
∴DE=CF,AF=BE,
∵A(1,1),C(2,3),B(4,1),
∴DE=CF=2,AE=4-AF=4-1=3,
∴D点坐标为(3,-1),
综上可知D点坐标为(-1,3)或(5,3)或(3,-1),
故答案为:(-1,3)或(5,3)或(3,-1).
点评 本题主要考查平行四边形的性质,掌握平行四边形的对边平行且相等是解题的关键,利用条件先确定出D点的位置是解题的突破口.

练习册系列答案
相关题目
1.二次根式$\sqrt{2x+1}$中x的取值范围是( )
| A. | x≥-$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$ |
13.若代数式x2-6x+b可化为(x-a)2-1,则b+a的值( )
| A. | 3 | B. | 4 | C. | 11 | D. | 6 |
10.若α,β是方程x2-2x-2=0的两个实数根,则α2+β2的值为( )
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
17.在数学课上,同学们都判断出命题“若m<n,则m2<${n}^{{2}^{m}}$”是假命题,下列是四位同学举出的反例,其中不正确的是( )
| A. | m=-1,n=2 | B. | m=-5,n=2 | C. | m=-4,n=-2 | D. | m=-8,n=-2 |
7.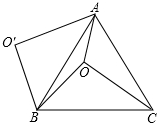 如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$
如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$
其中正确的有( )
 如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$
如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$其中正确的有( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
11.某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,如图记录的是这两名同学5次投篮中所投中的个数.
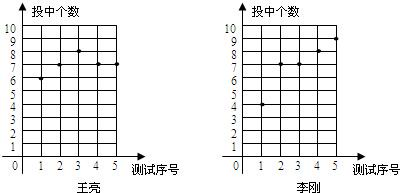
(1)请你根据图中的数据,填写表格;
(2)若你是教练,你打算选谁?简要说明理由.

(1)请你根据图中的数据,填写表格;
| 姓名 | 平均数 | 众数 | 方差 |
| 王亮 | 7 | 7 | 0.4 |
| 李刚 | 7 | 7 | 2.8 |
 如图,在△ABC中,AB=AC,∠BAC=90°,点D是BC上一点,DE∥AB,AE∥BC,DE分别交AC、AE于点O和E,连接AD、CE.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是BC上一点,DE∥AB,AE∥BC,DE分别交AC、AE于点O和E,连接AD、CE.