题目内容
 如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点.设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=24,则S△ADF-S△BEF=( )
如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点.设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=24,则S△ADF-S△BEF=( )| A、2 | B、4 | C、6 | D、8 |
考点:三角形的面积
专题:计算题
分析:利用三角形面积公式,等高的三角形的面积比等于底边的比,则S△AEC=
S△ABC=16,S△BCD=
S△ABC=12,然后利用S△AEC-S△BCD=4即可得到答案.
| 2 |
| 3 |
| 1 |
| 2 |
解答:解:∵EC=2BE,
∴S△AEC=
S△ABC=
×24=16,
∵点D是AC的中点,
∴S△BCD=
S△ABC=
×24=12,
∴S△AEC-S△BCD=4,
即S△ADF+S四边形CEFD-(S△BEF-S四边形CEFD)=4,
∴S△ADF-S△BEF=4.
故选B.
∴S△AEC=
| 2 |
| 3 |
| 2 |
| 3 |
∵点D是AC的中点,
∴S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AEC-S△BCD=4,
即S△ADF+S四边形CEFD-(S△BEF-S四边形CEFD)=4,
∴S△ADF-S△BEF=4.
故选B.
点评:本题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半,即S△=
×底×高;三角形的中线将三角形分成面积相等的两部分.
| 1 |
| 2 |

练习册系列答案
相关题目
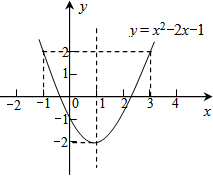 已知二次函数y=x2-2x-1的图象如图所示,根据图中提供的信息,求使得y≤2成立的x的取值范围是( )
已知二次函数y=x2-2x-1的图象如图所示,根据图中提供的信息,求使得y≤2成立的x的取值范围是( )| A、x≤-1或x≥3 |
| B、-2≤x≤2 |
| C、x≥-2 |
| D、-1≤x≤3 |
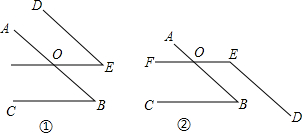
 如图,点O是?ABCD对角线AC中点,EF经过点O交AD于点E,交BC于点F,连接BE,DF
如图,点O是?ABCD对角线AC中点,EF经过点O交AD于点E,交BC于点F,连接BE,DF 已知△ABC,AB=AC=5cm,BC=8cm,P为AC上一动点,沿着折线CAB运动(当到达B时停止),Q为CB上一动点,沿CB运动(到B时停止),若P,Q分别同时从C点出发,以2cm/s和1cm/s的速度沿折线CAB和CB运动,问,何时PQ截△ABC两边所形成的三角形与原三角形相似?是位似图形吗?
已知△ABC,AB=AC=5cm,BC=8cm,P为AC上一动点,沿着折线CAB运动(当到达B时停止),Q为CB上一动点,沿CB运动(到B时停止),若P,Q分别同时从C点出发,以2cm/s和1cm/s的速度沿折线CAB和CB运动,问,何时PQ截△ABC两边所形成的三角形与原三角形相似?是位似图形吗? 如图是一个多边形,求∠A1+∠A2+∠A3+…+∠A23+∠A24的度数.
如图是一个多边形,求∠A1+∠A2+∠A3+…+∠A23+∠A24的度数.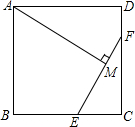 已知:E,F分别是正方形ABCD的边BC,CD上的点,AM⊥EF,垂足为M,AM=AB,
已知:E,F分别是正方形ABCD的边BC,CD上的点,AM⊥EF,垂足为M,AM=AB, 有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由.
有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由. 如图,在△ABC中,AB=AC,∠BAC=90°,BC=8,⊙A与BC相切于点D,且与AB、AC分别交于点E、F,则劣弧
如图,在△ABC中,AB=AC,∠BAC=90°,BC=8,⊙A与BC相切于点D,且与AB、AC分别交于点E、F,则劣弧