题目内容
已知一个立体图形,其正视图和侧视图均为等腰三角形,俯视图为半径为1cm的圆(含圆心),若它的侧面展开图的面积为2πcm2,则此几何体的高为
- A.
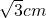
- B.2cm
- C.
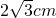
- D.4cm
A
分析:先由三视图判断几何体为圆锥,圆锥的侧面积=π×底面半径×母线长,先求出母线长,再根据勾股定理求出此几何体的高.
解答:∵圆锥的底面半径为1cm,侧面展开图的面积为2πcm2,
∴圆锥的母线长=2π÷π=2,
∴此几何体的高为= =
= .
.
故选A.
点评:考查勾股定理、由三视图判断几何体,圆锥的侧面积的计算公式,用到的知识点为:圆锥的侧面积=π×底面半径×母线长.
分析:先由三视图判断几何体为圆锥,圆锥的侧面积=π×底面半径×母线长,先求出母线长,再根据勾股定理求出此几何体的高.
解答:∵圆锥的底面半径为1cm,侧面展开图的面积为2πcm2,
∴圆锥的母线长=2π÷π=2,
∴此几何体的高为=
 =
= .
.故选A.
点评:考查勾股定理、由三视图判断几何体,圆锥的侧面积的计算公式,用到的知识点为:圆锥的侧面积=π×底面半径×母线长.

练习册系列答案
相关题目