题目内容
如图，在等边△ABC中，M、N分别是边AB，AC的中点，D为MN的中点，CD，BD的延长线分别交
于AB，AC于点E，点F，下列结论正确的是
①MN的长是BC的
；
②△EMD的面积是△ABC面积的
；
③EM和FN的长度相等；
④图中全等的三角形有4对；
⑤连接EF，则四边形EBCF一定是等腰梯形．
- A.①②⑤
- B.①③④
- C.①②④
- D.①③⑤
D
分析：根据等腰梯形的性质及全等三角形的判定等知识对各个结论进行分析从而得到答案．
解答：①由三角形的中位线可得，故正确；
②无法得到此结论，故不正确；
③利用ASA可判定△EMD≌△FND，从而可得到EM=FN，故正确；
④其5对，分别是：△BDM≌△CDN，△DME≌△DNF，△BDE≌△CDF，△ABF≌△ACE，△BCE≌△CBF，故不正确；
⑤可通过证明三角形全等得到BE=CF且EF∥BC，从而推出四边形EBCF一定是等腰梯形，故正确；
所以正确的有①③⑤，故选D．
点评：此题主要考查学生对等腰梯形的判定及全等三角形的判定等知识点的理解及运用．
分析：根据等腰梯形的性质及全等三角形的判定等知识对各个结论进行分析从而得到答案．
解答：①由三角形的中位线可得，故正确；
②无法得到此结论，故不正确；
③利用ASA可判定△EMD≌△FND，从而可得到EM=FN，故正确；
④其5对，分别是：△BDM≌△CDN，△DME≌△DNF，△BDE≌△CDF，△ABF≌△ACE，△BCE≌△CBF，故不正确；
⑤可通过证明三角形全等得到BE=CF且EF∥BC，从而推出四边形EBCF一定是等腰梯形，故正确；
所以正确的有①③⑤，故选D．
点评：此题主要考查学生对等腰梯形的判定及全等三角形的判定等知识点的理解及运用．
练习册系列答案
金钥匙试卷系列答案
相关题目
16、如图，在等边△ABC的边BC上任取一点D，作∠ADE=60°，DE交∠C的外角平分线于E，则△ADE是
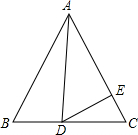如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的面积为（ ）A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
21、如图，在等边△ABC中，AD是∠BAC的平分线，点E在AC边上，且∠EDC=15°．
如图，在等边△ABC中，D是AC的中点，延长BC到点E，使CE=CD，AB=10cm．
如图，在等边△ABC中，BF是高，D是BF上一点，且OF=AF，作OE⊥BF，垂足为D，且OE=OB，连AE、AO、BE，求证：