Question

9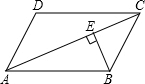．如图，在?ABCD中，AC=24，BE⊥AC于点E，BE=5，AD=8，则两平行线AD与BC间的距离是15．

Answer 1

分析 根据平行四边形的性质可证出△ADC≌△CBA，然后可得S_{平行四边形ABCD}=120，过B作BF⊥AD，利用面积可得答案．

解答 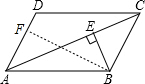解：∵四边形ABCD是平行四边形，
∴AD=BC，DC=AB，
在△ADC和△CBA中$\left\{\begin{array}{l}{AD=BC}\\{AC=AC}\\{DC=AB}\end{array}\right.$，
∴△ADC≌△CBA（SSS），
∵AC=24，BE=5，
∴S_△ACB=$\frac{1}{2}×24×5$=60，
∴S_△ADC=60，
∴S_{平行四边形ABCD}=120，
过B作BF⊥AD，
∵AD=8，
∴8BF=120，
解得：BF=15．
故答案为：15．

点评 此题主要考查了平行四边形的性质，关键是掌握平行四边形的面积公式：底×高，平行四边形对边相等．