Question

7．如图，隧道的截面由抛物线ADC和矩形AOBC构成，矩形的长OB是12m，
宽OA是4m．拱顶D到地面OB的距离是10m．若以O原点，OB所在的直线为x轴，OA所在的直线为y轴，建立直角坐标系．
（1）画出直角坐标系xOy，并求出抛物线ADC的函数表达式；
（2）在抛物线型拱壁E、F处安装两盏灯，它们离地面OB的高度都是8m，则这两盏灯的水平距离EF是多少米？

Answer 1

分析 （1）根据所建坐标系易求抛物线ADC的顶点坐标和A的坐标解答即可；
（2）把y=8代入表达式中运用函数性质求解即可．

解答 解：（1）画出直角坐标系xOy，如图：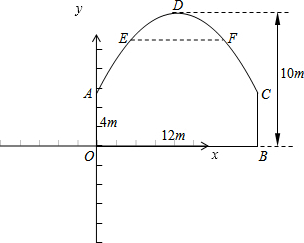

由题意可知，抛物线ADC的顶点坐标为（6，10），
A点坐标为（0，4），
可设抛物线ADC的函数表达式为y=a（x-6）²+10，
将x=0，y=4代入得：a=-$\frac{1}{6}$，
∴抛物线ADC的函数表达式为：y=-$\frac{1}{6}$ （x-6）²+10． 
（2）由y=8得：-$\frac{1}{6}$ （x-6）²+10=8，
解得：x₁=6+2$\sqrt{3}$，x₂=6-2$\sqrt{3}$，
则EF=x₁-x₂=4$\sqrt{3}$，即两盏灯的水平距离EF是4$\sqrt{3}$米．

点评 此题主要考查了二次函数的应用，关键在根据图形特点选取一个合适的参数表示它们，得出关系式后运用函数性质来解．