题目内容
9.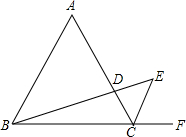 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.求证:△ABD∽△CED.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.求证:△ABD∽△CED.
分析 利用等边三角形的性质得出∠BAC=∠ACB=60°,∠ACF=120°,进而结合角平分线的性质得出∠BAC=∠ACE,进而得出答案.
解答 证明:∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,∠ACF=120°,
∵CE是外角平分线,
∴∠ACE=60°,
∴∠BAC=∠ACE,
又∵∠ADB=∠CDE,
∴△ABD∽△CED.
点评 此题主要考查了相似三角形的判定以及等边三角形的性质,根据题意得出∠BAC=∠ACE是解题关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
19.下列各式中的最简分式是( )
| A. | $\frac{3y}{5}$ | B. | $\frac{{a}^{2}b+1}{a{b}^{2}-1}$ | C. | $\frac{a+b}{(a+b)^{2}}$ | D. | $\frac{{a}^{2}+2a+1}{{a}^{2}-1}$ |
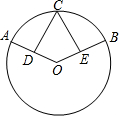 如图,在⊙O中,点C是$\widehat{AB}$的中点,D、E分别是半径OA和OB的中点,求证:CD=CE.
如图,在⊙O中,点C是$\widehat{AB}$的中点,D、E分别是半径OA和OB的中点,求证:CD=CE.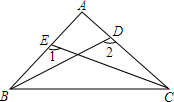 如图,已知BD=CE,∠1=∠2,求证:AB=AC.
如图,已知BD=CE,∠1=∠2,求证:AB=AC.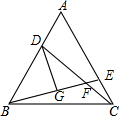 已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证:
已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证:
 计算与化简:
计算与化简: