题目内容
下列语句:①相等的圆周角所对的弧是等弧;②经过三个点一定可以作一个圆;③等腰直角三角形的外心不在这个三角形顶角的角平分线上;④等边三角形的内心到三角形三个顶点的距离相等,正确的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:圆周角定理,确定圆的条件,三角形的外接圆与外心,三角形的内切圆与内心
专题:
分析:由圆周角定理,可得在同圆或等圆中,相等的圆周角所对的弧是等弧;由确定三角形的条件可知经过不在同一直线上三个点一定可以作一个圆;由三角形的外心与内心的知识可知等腰直角三角形的外心在这个三角形顶角的角平分线上,等边三角形的内心到三角形三个顶点的距离相等.
解答:解:①在同圆或等圆中,相等的圆周角所对的弧是等弧,故错误;
②经过不在同一直线上三个点一定可以作一个圆;故错误;
③等腰直角三角形的外心在这个三角形顶角的角平分线上;故错误;
④等边三角形的内心到三角形三个顶点的距离相等;正确.
故选A.
②经过不在同一直线上三个点一定可以作一个圆;故错误;
③等腰直角三角形的外心在这个三角形顶角的角平分线上;故错误;
④等边三角形的内心到三角形三个顶点的距离相等;正确.
故选A.
点评:此题考查了圆周角定理、确定圆的条件以及三角形外心与外心的知识.此题难度不大,注意熟记定理是解此题的关键.

练习册系列答案
相关题目
计算-5+6的结果是( )
| A、-1 | B、1 | C、-5 | D、-6 |
在同圆中,若AB和CD都是劣弧,且AB=2CD,那么弦AB和CD的大小关系是( )
| A、AB=2CD |
| B、AB>2CD |
| C、AB<2CD |
| D、无法比较它们的大小 |

 如图所示,AB=AC,∠B=∠C,点D、E分别在AB、AC上,且点F是DE的中点,求证:AF⊥DE.
如图所示,AB=AC,∠B=∠C,点D、E分别在AB、AC上,且点F是DE的中点,求证:AF⊥DE.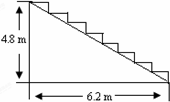 遂昌元立大酒店在重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼道宽2m,其侧面如图所示,则购买地毯至少需要
遂昌元立大酒店在重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼道宽2m,其侧面如图所示,则购买地毯至少需要