题目内容
19．
如图，以正方形ABCD的对角线AC为一边作菱形AEFC，则∠FAB=22.5°．
分析 根据正方形的性质可得出∠CAB=45°，根据菱形的性质可得出AF平分∠CAB，从而得出∠FAB的度数．
解答 解：∵四边形ABCD为正方形，AC为对角线，
∴∠DAC=∠CAB=45°．
∵四边形AEFC为菱形，AF为对角线，
∴AF平分∠CAB，
∴∠FAB=$\frac{1}{2}$∠CAB=22.5°．
故答案为：22.5°．
点评 本题考查了正方形的性质以及菱形的性质，解题的关键是根据菱形的性质找出AF平分∠CAB．本题属于基础题，难度不大，解决该题型题目时，牢记各特殊图形的性质是关键．
练习册系列答案
相关题目
17．
如图，△ABC≌△AEF，那么与∠EAC相等的角是（ ）
如图，△ABC≌△AEF，那么与∠EAC相等的角是（ ）| A． | ∠ACB | B． | ∠BAF | C． | ∠CAF | D． | ∠AFE |
已知：矩形ABCD内一点N，△ANB为等腰直角三角形，连结BN、CN并延长分别交DC，AD于点E，M，在AB上截取BF=EC，连接MF．
如图，在△ABC中，∠B=∠C，∠BAC=80°，AD∥EF，∠1=∠2，求∠BDG的度数．
9．
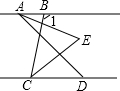如图，己知 AB∥CD，∠BAD 和∠BCD 的平分线交于点E，∠1=100°，∠BAD=m°，则∠AEC的度数为（ ）
如图，己知 AB∥CD，∠BAD 和∠BCD 的平分线交于点E，∠1=100°，∠BAD=m°，则∠AEC的度数为（ ）| A． | m° | B． | （40+$\frac{m}{2}$）° | C． | （40-$\frac{m}{2}$）° | D． | （50+$\frac{m}{2}$）° |