题目内容
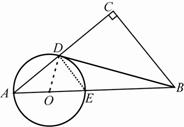
在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
 |
解:(1)直线BD与⊙O的位置关系是相切.
证明:连结OD,DE.
∵∠C=90°,
∴∠CBD +∠CDB=90°.
∵∠A=∠CBD,
∴∠A+∠CDB=90°.
 ∵OD = OA,
∵OD = OA,
∴∠A=∠ADO.
∴∠ADO + ∠CDB=90°.
∴∠ODB = 180° - 90°=90°.
∴OD⊥BD.
∵OD为半径,
∴BD是⊙O切线.
(2)∵AD : AO=8 : 5,
∴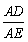 =
=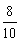 .
.
∴由勾股定理得AD : DE : AE = 8 : 6 : 10.
∵∠C=90°,∠CBD=∠A.
∴△BCD∽△ADE.
∴DC : BC : BD= DE : AD : AE=6 : 8 : 10.
∵BC=3,
∴BD= .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 图象的顶点坐标是
图象的顶点坐标是  B.
B. C.
C. D.
D.
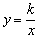 的图象的一个交点为A(1 , m).
的图象的一个交点为A(1 , m).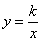 的解析式;
的解析式; 的坐标(不写求解过程).
的坐标(不写求解过程). 解:
解: 有两个不相等的实数根,则实数k的取值范围 是 .
有两个不相等的实数根,则实数k的取值范围 是 . 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8). 的值是( )
的值是( )  D.6
D.6
 的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.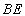 .求证:
.求证: ;
;