题目内容
9.已知反比例函数y1=$\frac{k}{x}$(k≠0)和一次函数y2=-x.(1)当k满足什么条件时,这两个函数的图象有两个不同的交点?
(2)若一次函数和反比例函数的图象交于点(-3,m)
①求m和k的值;
②根据函数图象回答:当y1>y2时,x的取值范围是什么?
分析 (1)函数的图象有两个不同的交点,即两个解,用二次函数根的判别式可解;
(2)①两个函数交点的坐标满足这两个函数关系式,因此将交点的坐标分别代入反比例函数关系式和一次函数关系式即可求得待定的系数,从而求得m和k的值;②根据函数图象和交点坐标,即可求得x的取值范围.
解答 解:(1)由联立方程组$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y=-x}\end{array}\right.$,
有-x=$\frac{k}{x}$,即x2+k=0.
要使两个函数的图象有两个不同的交点,须使方程x2+k=0有两个不相等的实数根.
∴△=02-4k=-4k>0,
解得k<0.
∴当k<0时,这两个函数的图象有两个不同的交点;
(2)①∵一次函数和反比例函数的图象交于点(-3,m),
∴$\left\{\begin{array}{l}{m=-\frac{k}{3}}\\{m=-(-3)}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-9}\\{m=3}\end{array}\right.$.
∴m=3,k=-9;
②∵一次函数和反比例函数的图象交于点(-3,3)
∴另一个交点为(3,-3),
根据反比例函数y1=-$\frac{9}{x}$和一次函数y2=-x,画出函数的图象如图: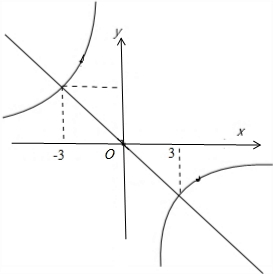
由图象可知y1>y2时,x的取值范围是-3<x<0或x>3.
点评 本题综合考查一次函数和反比例函数的交点问题,先由点的坐标根据待定系数法求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
相关题目
1. 如图,一个三角板的直角顶点放在直尺的一条边上,∠2=70°,那么∠1的度数是( )
如图,一个三角板的直角顶点放在直尺的一条边上,∠2=70°,那么∠1的度数是( )
 如图,一个三角板的直角顶点放在直尺的一条边上,∠2=70°,那么∠1的度数是( )
如图,一个三角板的直角顶点放在直尺的一条边上,∠2=70°,那么∠1的度数是( )| A. | 70° | B. | 30° | C. | 20° | D. | 15° |
18.2014年11月北京主办了第二十二届APEC(亚太经合组织)领导人会议,“亚太经合组织”联通太平洋两岸,从地理概念上逐渐变成了一个拥有28000000人口的经济合作体,把“28000000”用科学记数法表示正确的是( )
| A. | 2.8×107 | B. | 2.8×109 | C. | 28×108 | D. | 28×107 |
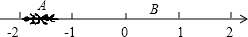 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.
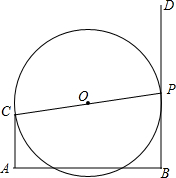 如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为$\frac{9}{2}$.
如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为$\frac{9}{2}$.