题目内容
8. 如图,在?ABCD中,点E、F分别在边AD、BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )个.
如图,在?ABCD中,点E、F分别在边AD、BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先利用平行四边形的性质得到CD∥AB,AD∥BC,则根据平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似可判断△DGM∽△AGB,△DGM∽△CBM,再利用EF∥CD可判断△DGM∽△EGN,△CBM∽△FBN,然后根据相似的传递性可得到答案.
解答 解:如图,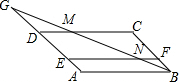
∵四边形ABCD为平行四边形,
∴CD∥AB,AD∥BC,
∴△DGM∽△AGB,△DGM∽△CBM,
∵EF∥CD,
∴△DGM∽△EGN,△CBM∽△FBN,
∴△DGM∽△AGB∽△FBN∽△CBM∽△EGN.
故选D.
点评 本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.解决的关键是利用平行四边形的性质得到直线平行,注意不要漏掉相似三角形.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
16.若a<b,则下列不等式中成立的是( )
| A. | a-b>0 | B. | a-2<b-2 | C. | $\frac{1}{2}$a>$\frac{1}{2}$b | D. | -2a<-2b |
3.tan60°=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
20.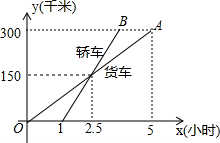 如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )
如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )
 如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )
如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )| A. | 1小时 | B. | 2小时 | C. | 3小时 | D. | 4小时 |
17. 如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )
如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )
 如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )
如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )| A. | 20cm | B. | 18cm | C. | 16cm | D. | 10cm |
 如图是一个由6个相同的小立方体组成的几何体,从上面看得到的平面图形是( )
如图是一个由6个相同的小立方体组成的几何体,从上面看得到的平面图形是( )



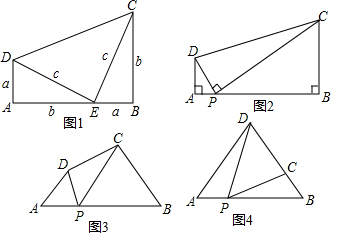 如图1是美国第20届总统加菲尔德于1876年公开发表的勾股定理一个简明证法,聪明的思齐和他的社团小朋友们发现:两个直角三角形在发生变化过程中,只要满足一定的条件,就会有神奇的结果:
如图1是美国第20届总统加菲尔德于1876年公开发表的勾股定理一个简明证法,聪明的思齐和他的社团小朋友们发现:两个直角三角形在发生变化过程中,只要满足一定的条件,就会有神奇的结果: