题目内容
10. 如图,将三角形纸板ABC沿直线AB向右平行移动,使∠CAB到达∠DBE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
如图,将三角形纸板ABC沿直线AB向右平行移动,使∠CAB到达∠DBE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 100° |
分析 根据平移的性质得出AC∥BE,以及∠CAB=∠EBD=50°,进而求出∠CBE的度数.
解答 解:∵将△ABC沿直线AB向右平移后到达△BDE的位置,
∴AC∥BE,
∴∠CAB=∠EBD=50°,
∵∠ABC=100°,
∴∠CBE的度数为:180°-50°-100°=30°.
故选C.
点评 此题主要考查了平移的性质以及三角形内角和定理,得出∠CAB=∠EBD=50°是解决问题的关键.

练习册系列答案
相关题目
20.下列调查中,最适宜采用全面调查方式的是( )
| A. | 对广水市中学生每天学习所用时间的调查 | |
| B. | 对全国中学生心理健康现状的调查 | |
| C. | 对某班学生进行6月5日是“世界环境日”知晓情况的调查 | |
| D. | 对广水市初中学生视力情况的调查 |
15. 如图,在△ABC中,AB=AC,∠BAC=108°,AD、AE将∠BAC三等分交边BC于点D,点E,则下列结论中错误的是( )
如图,在△ABC中,AB=AC,∠BAC=108°,AD、AE将∠BAC三等分交边BC于点D,点E,则下列结论中错误的是( )
 如图,在△ABC中,AB=AC,∠BAC=108°,AD、AE将∠BAC三等分交边BC于点D,点E,则下列结论中错误的是( )
如图,在△ABC中,AB=AC,∠BAC=108°,AD、AE将∠BAC三等分交边BC于点D,点E,则下列结论中错误的是( )| A. | $\frac{BD}{DE}$=$\frac{\sqrt{5}-1}{2}$ | B. | 点D是线段BC的黄金分割点 | ||
| C. | 点E是线段BC的黄金分割点 | D. | 点E是线段CD的黄金分割点 |
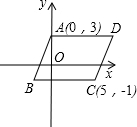 如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1).
如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1). 有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形.请探究筝形的性质与判定方法.
有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形.请探究筝形的性质与判定方法.