题目内容
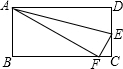如图，分别在长方形ABCD的边DC，BC上取两点E，F，使得AE平分∠DAF，若∠BAF=60°，则∠DAE=
- A.45°
- B.30°
- C.15°
- D.60°
C
分析：长方形内角为90°，已知∠BAF=60°，所以可以得到∠DAF，又因为AE平分∠DAF，所以∠DAE便可求出．
解答：在长方形ABCD中，∠BAD=90°
∵∠BAF=60°
∴∠DAF=90°-∠BAF=30°
又AE平分∠DAF
所以∠DAE=
∠DAF=15°
故选C．
点评：运用了长方形的四个角都是直角以及角平分线的概念即可解决．
分析：长方形内角为90°，已知∠BAF=60°，所以可以得到∠DAF，又因为AE平分∠DAF，所以∠DAE便可求出．
解答：在长方形ABCD中，∠BAD=90°
∵∠BAF=60°
∴∠DAF=90°-∠BAF=30°
又AE平分∠DAF
所以∠DAE=
∠DAF=15°故选C．
点评：运用了长方形的四个角都是直角以及角平分线的概念即可解决．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
如图，分别在长方形ABCD的边DC，BC上取两点E，F，使得AE平分∠DAF，若∠BAF=60°，则∠DAE=（ ）| A、45° | B、30° | C、15° | D、60° |
=n，其中0＜n≤1．
=______；
（M为AD的中点），m的值发生变化时，求证：EP=AE+DP；
的值是否发生变化？说明理由．