题目内容
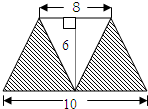
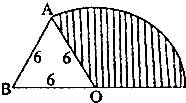
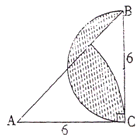
求阴影部分面积.(单位:cm)
解:3.14× ÷2-[6×6÷2-
÷2-[6×6÷2-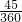 ×3.14×62],
×3.14×62],
=14.13-[18-14.13],
=14.13-3.87,
=10.26(平方厘米);
答:阴影部分的面积是10.26平方厘米.
分析:观察图形可知,阴影部分的面积等于图中半圆的面积减去空白处1的面积,由此利用半圆的面积公式求出半圆的面积是:3.14× ÷2=14.13平方厘米,只要再求出空白处1的面积即可解答;因为三角形ABC是等腰直角三角形,所以∠A=45度,则空白处1的面积=三角形ABC的面积-圆心角是45度,半径是6厘米的扇形的面积,由此利用三角形和扇形的面积公式即可解答.
÷2=14.13平方厘米,只要再求出空白处1的面积即可解答;因为三角形ABC是等腰直角三角形,所以∠A=45度,则空白处1的面积=三角形ABC的面积-圆心角是45度,半径是6厘米的扇形的面积,由此利用三角形和扇形的面积公式即可解答.
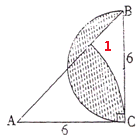
点评:解决此题的关键是利用等积转换,即等底等高的三角形面积相等,将阴影部分重组,从而利用已知条件求得阴影部分的面积.
 ÷2-[6×6÷2-
÷2-[6×6÷2-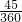 ×3.14×62],
×3.14×62],=14.13-[18-14.13],
=14.13-3.87,
=10.26(平方厘米);
答:阴影部分的面积是10.26平方厘米.
分析:观察图形可知,阴影部分的面积等于图中半圆的面积减去空白处1的面积,由此利用半圆的面积公式求出半圆的面积是:3.14×
 ÷2=14.13平方厘米,只要再求出空白处1的面积即可解答;因为三角形ABC是等腰直角三角形,所以∠A=45度,则空白处1的面积=三角形ABC的面积-圆心角是45度,半径是6厘米的扇形的面积,由此利用三角形和扇形的面积公式即可解答.
÷2=14.13平方厘米,只要再求出空白处1的面积即可解答;因为三角形ABC是等腰直角三角形,所以∠A=45度,则空白处1的面积=三角形ABC的面积-圆心角是45度,半径是6厘米的扇形的面积,由此利用三角形和扇形的面积公式即可解答.
点评:解决此题的关键是利用等积转换,即等底等高的三角形面积相等,将阴影部分重组,从而利用已知条件求得阴影部分的面积.

练习册系列答案
相关题目
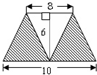 两个完全一样的直角梯形如下叠放,求阴影部分面积.(单位:cm)
两个完全一样的直角梯形如下叠放,求阴影部分面积.(单位:cm)