题目内容
15.一段公路,甲队单独修要用20天,乙队单独修要30天,如果两队合作,每天完成这项工程的$\frac{1}{12}$,12天可以完成.分析 首先根据工作效率=工作量÷工作时间,分别求出甲乙的工作效率各是多少;然后把甲乙的工作效率求和,求出两队合作,每天完成这项工程的几分之几;最后工作时间=工作量÷工作效率,用1除以甲乙的工作效率之和,求出两队合作多少天完成即可.
解答 解:$\frac{1}{20}+\frac{1}{30}=\frac{1}{12}$
1$÷\frac{1}{12}=12(天)$
答:两队合作,每天完成这项工程的$\frac{1}{12}$,12天可以完成.
故答案为:$\frac{1}{12}、12$.
点评 此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率,解答此题的关键是求出甲乙的工作效率各是多少.

练习册系列答案
相关题目
10.用4个同样大小的正方体摆成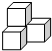 ,从( )看到的是
,从( )看到的是 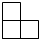 .
.
 ,从( )看到的是
,从( )看到的是  .
.| A. | 正面 | B. | 侧面 | C. | 上面 |