题目内容
一枝长18厘米的圆柱形铅笔,底面直径是0.6厘米,把铅笔的笔头削成高是2厘米的圆锥形后,铅笔的体积减少了多少立方厘米?
解:圆柱形底面半径为:0.6÷2=0.3(厘米),
铅笔减数的体积为:3.14×0.32×2-3.14×0.32×2×
=3.14×0.09×2-3.14×0.09×2× ,
,
=0.2826×2-0.2826×2× ,
,
=0.5652-0.5652× ,
,
=0.5652-0.1884,
=0.3768(立方厘米);
答:铅笔的体积减少了0.3768平方厘米.
分析:根据题意,可把长18厘米的圆柱形铅笔分为两部分,底面积不变,长(18-2)厘米为一部分圆柱,长2厘米的为另一部分圆柱,其中第一部分的圆柱形铅笔的体积没有变化不用计算,这根铅笔减少的体积等于第二部分的圆柱形的体积减去削成的圆锥的体积,列式即可得到答案.
点评:此题主要考查的是圆锥的体积公式v=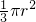 和圆柱的体积公式V=πr2的应用.
和圆柱的体积公式V=πr2的应用.
铅笔减数的体积为:3.14×0.32×2-3.14×0.32×2×

=3.14×0.09×2-3.14×0.09×2×
 ,
,=0.2826×2-0.2826×2×
 ,
,=0.5652-0.5652×
 ,
,=0.5652-0.1884,
=0.3768(立方厘米);
答:铅笔的体积减少了0.3768平方厘米.
分析:根据题意,可把长18厘米的圆柱形铅笔分为两部分,底面积不变,长(18-2)厘米为一部分圆柱,长2厘米的为另一部分圆柱,其中第一部分的圆柱形铅笔的体积没有变化不用计算,这根铅笔减少的体积等于第二部分的圆柱形的体积减去削成的圆锥的体积,列式即可得到答案.
点评:此题主要考查的是圆锥的体积公式v=
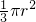 和圆柱的体积公式V=πr2的应用.
和圆柱的体积公式V=πr2的应用. 
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目

 x=4.9+
x=4.9+ x
x +
+ -x=2
-x=2 =2x+
=2x+
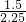 =9.6﹕x
=9.6﹕x