题目内容
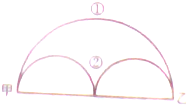 如图,从甲地到乙地有2条路可走,两条路相比,( )近.
如图,从甲地到乙地有2条路可走,两条路相比,( )近.分析:如下图:AB为大半圆的直径,AC和BC分别为两个小半圆的直径,观察图形为,第一条路的长度就是这个小半圆的弧长,第二条路,就是大半圆的弧长;据此利用圆的周长公式分别计算出来,再进行比较即可
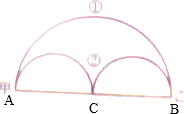

解答:解:大半圆的周长为:π×AB÷2=
πAB,
两个小半圆的周长的和为:π×AC÷2+π×BC÷2,
=
πAC+
πBC,
=
π(AC+BC),
=
πAB,
所以大半圆的弧长等于两个小半圆的弧长之和;
故选:C.
| 1 |
| 2 |
两个小半圆的周长的和为:π×AC÷2+π×BC÷2,
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
所以大半圆的弧长等于两个小半圆的弧长之和;
故选:C.
点评:设出圆的直径,利用直径之间的关系和圆周长的计算方法分别表示出大、小圆的弧长是解答此题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 (2010?龙湖区)如图,从甲地到乙地有2条路可走,从乙地到丙地有4条路可走,那么从甲地经乙地到丙地,有( )条不同的路可走.
(2010?龙湖区)如图,从甲地到乙地有2条路可走,从乙地到丙地有4条路可走,那么从甲地经乙地到丙地,有( )条不同的路可走. 如图,从甲地到乙地有两条路线,乙地到丁地也有两条路线;从甲地到丙地只有一条路线,丙地到丁地有三条路线.那么从甲地到丁地共有多少种不同走法?
如图,从甲地到乙地有两条路线,乙地到丁地也有两条路线;从甲地到丙地只有一条路线,丙地到丁地有三条路线.那么从甲地到丁地共有多少种不同走法?
 如图,从甲地到乙地有A、B两条路可走,这两条路的长度( )
如图,从甲地到乙地有A、B两条路可走,这两条路的长度( )