题目内容
6.某厂的工人中,女工比男工多$\frac{2}{3}$,后来又把45名男工换为女工,使得女工人数达到总人数的$\frac{20}{29}$,这时有多少名女工?分析 女工比男工多$\frac{2}{3}$,先,把男工人数看作单位“1”,则女工人数相当于女工人数的(1+$\frac{2}{3}$),总人数相当于男工人数的(1+1+$\frac{2}{3}$);根据“把45名男工换为女工”,可知男工、女工总人数不变,把男工、女工总人数看作单位“1”,那么女工占总人数的(1+$\frac{2}{3}$)÷(1+1+$\frac{2}{3}$)=$\frac{5}{8}$,则45人对应的分率为($\frac{20}{29}$-$\frac{5}{8}$),用除法求出总人数,然后用总人数乘上$\frac{20}{29}$即可求出这时有多少名女工.
解答 解:女工占总人数的:
(1+$\frac{2}{3}$)÷(1+1+$\frac{2}{3}$)
=$\frac{5}{3}$÷$\frac{8}{3}$
=$\frac{5}{8}$
总人数:
45÷($\frac{20}{29}$-$\frac{5}{8}$)
=45÷$\frac{15}{232}$
=696(名)
此时女工人数:
696×$\frac{20}{29}$=480(名)
答:这时有480名女工.
点评 本题的关键是根据总人数不变,再根据前后女工占总人数分率的变化求出女工是多少.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
16.9□968≈10万,□里最小可以填( )
| A. | 0 | B. | 5 | C. | 4 |
17.$\frac{3}{5}$千克小麦可以磨出$\frac{1}{2}$千克的面粉,那么1千克的小麦可以磨出$\frac{5}{6}$千克的面粉,磨1千克面粉需要小麦$\frac{6}{5}$千克.
1.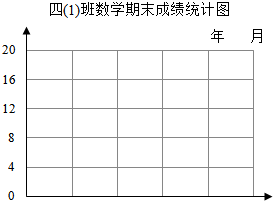 四(1)班上学期数学期末考试成绩整理如下:
四(1)班上学期数学期末考试成绩整理如下:
(1)根据上表中的数据,制作统计表和条形统计图.
四(1)班数学期末考试成绩统计表 年 月
(2)四(1)班的数学成绩在哪个分数段的人数最多,哪个分数段的人数最少?
 四(1)班上学期数学期末考试成绩整理如下:
四(1)班上学期数学期末考试成绩整理如下:| 100 分 | 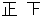 |
| 90〜99分 | 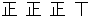 |
| 80〜89分 | 正正 |
| 70〜79分 | 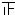 |
| 60〜69分 |  |
四(1)班数学期末考试成绩统计表 年 月
| 分数段 | 合计 | 100 | 90~99 | 80~89 | 70~79 | 60~69 |
| 人数 |
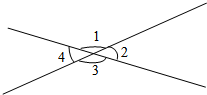 量出下面各角的度数,再填空.
量出下面各角的度数,再填空.