题目内容
有一座房子,长12米,宽8米,在房子外的一个墙角用一根长14米的绳子拴一条狗,这条狗活动的最大可能范围的面积是( )平方米.
分析:根据题意,狗的活动范围本来是一个圆,但是被房子挡住了一部分,但是拴狗绳分别大于房子的长与宽,所以狗能到达绳子比房子长、宽多出的地方,绳子的长比房子的宽多14-8=6米,比房子的长多14-12=2米,那么这条狗活动的范围就是:以14米为半径的圆的面积的
加上以4米为半径的圆的面积的
再加上以2米为半径的圆的面积的
,列式解答即可得到答案.
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:如图
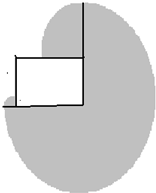
×142×3.14+
×22×3.14+
×62×3.14
=147×3.14+3.14+9×3.14,
=461.58+3.14+28.26,
=464.72+28.26,
=492.98(平方米);
答:这条狗的最大活动范围是492.98平方米.
故选:A.

| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
=147×3.14+3.14+9×3.14,
=461.58+3.14+28.26,
=464.72+28.26,
=492.98(平方米);
答:这条狗的最大活动范围是492.98平方米.
故选:A.
点评:解答此题的关键是确定分析出这条狗在比房子的长、宽处的活动范围,然后再进行计算即可.

练习册系列答案
相关题目