题目内容
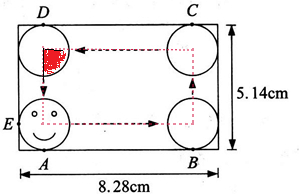
如图,有一个电动玩具,它有一个8.28×5.14的长方形盘(单位:cm)和一个半径为1厘米的小圆盘(盘中画有娃娃脸),它们的连接点为A,E.如果小圆盘沿着长方形内壁,从A点出发不停的滚动(无滑动),直到回到原来位置.

(1)小圆盘(娃娃脸)在B,C,D的位置是怎样的?请一一画出示意图.
(2)小圆盘共自转了几圈?
(3)计算小圆盘绕长方形盘滚动一周,扫过长方形盘的面积.

(1)小圆盘(娃娃脸)在B,C,D的位置是怎样的?请一一画出示意图.
(2)小圆盘共自转了几圈?
(3)计算小圆盘绕长方形盘滚动一周,扫过长方形盘的面积.
分析:(1)A到B转了(8.28-1-1)÷(2×3.14)=1(圈),娃娃脸在B位置同A位置;B到C转了(5.14-1-1)÷(2×3.14)=0.5(圈),娃娃脸在C位置与A位置相反(眼睛在下,嘴在上);C到D转了(8.28-1-1)÷(2×3.14)=1(圈),娃娃脸在D位置同C位置;D到A转了(5.14-1-1)÷(2×3.14)=0.5(圈),娃娃脸回到A位置时同原A位置(眼睛在上,嘴在下);
(2)小圆盘共自转了1+0.5+1+0.5=3(圈).
(3)观察图形可知,每个角上都正好转过一个
圆,所以四个角合起来正好是一个半径为1厘米的圆的面积;再加上2个长为8.28-2=6.28厘米,宽为2厘米的两个长方形的面积;和两个长5.14-2=3.14厘米,宽2厘米的长方形的面积;因为中间涂色位置的
圆的面积在两个长方形中重复相加了,所以再减去多加的这个半径为1厘米的圆的面积,实际这个圆转过的面积就是上面分析中的四个长方形的面积之和,据此即可解答.
(2)小圆盘共自转了1+0.5+1+0.5=3(圈).
(3)观察图形可知,每个角上都正好转过一个
| 1 |
| 4 |
| 1 |
| 4 |

解答:解:(1)A到B转了(8.28-1-1)÷(2×3.14)=1(圈),娃娃脸同A;
B到C转了(5.14-1-1)÷(2×3.14)=0.5(圈),娃娃与A上下相反;
C到D转了(8.28-1-1)÷(2×3.14)=1(圈),娃娃脸同C;
D到A转了(5.14-1-1)÷(2×3.14)=0.5(圈),娃娃脸回到A位置;
(2)小圆盘共自转了1+0.5+1+0.5=3(圈);
画图如下:
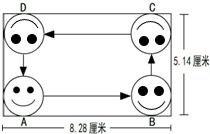 ,
,
(3)8.28-2=6.28(厘米),
5.14-2=3.14(厘米),
6.28×2+3.14×2,
=12.56+6.28,
=18.84(平方厘米),
答:转过的面积是18.84平方厘米.
B到C转了(5.14-1-1)÷(2×3.14)=0.5(圈),娃娃与A上下相反;
C到D转了(8.28-1-1)÷(2×3.14)=1(圈),娃娃脸同C;
D到A转了(5.14-1-1)÷(2×3.14)=0.5(圈),娃娃脸回到A位置;
(2)小圆盘共自转了1+0.5+1+0.5=3(圈);
画图如下:
 ,
,(3)8.28-2=6.28(厘米),
5.14-2=3.14(厘米),
6.28×2+3.14×2,
=12.56+6.28,
=18.84(平方厘米),
答:转过的面积是18.84平方厘米.
点评:本题的知识点有:旋转、圆的周长等.小圆盘(娃娃脸)在B、C、D位置是怎样的,关键是看转了几圈.解答(3)题的关键是把滚过的面积分割拼凑为圆形与长方形解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
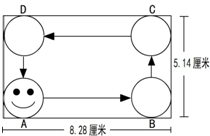 有一个电动玩具,它有一个8.28×5.14的长方形盘(单位:厘米)和一个半径为1厘米的小圆盘(盘中画有娃娃脸)它们的连接点为A、B(如图)如果小圆盘沿着长方形内壁,从A点出发,不停的滚动(无滑动),最后回到原来位置,请你计算一下,小圆盘(娃娃脸)在B、C、D位置是怎样的,并请画出示意图?小圆盘共自转了几圈?
有一个电动玩具,它有一个8.28×5.14的长方形盘(单位:厘米)和一个半径为1厘米的小圆盘(盘中画有娃娃脸)它们的连接点为A、B(如图)如果小圆盘沿着长方形内壁,从A点出发,不停的滚动(无滑动),最后回到原来位置,请你计算一下,小圆盘(娃娃脸)在B、C、D位置是怎样的,并请画出示意图?小圆盘共自转了几圈?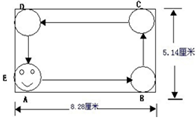 There is an electric toy formed by a rectangles(8.28cm×5.14cm)and a circle of radius 3cm(with a baby face on it),they connect at Ponint A
There is an electric toy formed by a rectangles(8.28cm×5.14cm)and a circle of radius 3cm(with a baby face on it),they connect at Ponint A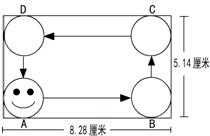 有一个电动玩具,它有一个8.28×5.14的长方形盘(单位:厘米)和一个半径为1厘米的小圆盘(盘中画有娃娃脸)它们的连接点为A、B(如图)如果小圆盘沿着长方形内壁,从A点出发,不停的滚动(无滑动),最后回到原来位置,请你计算一下,小圆盘(娃娃脸)在B、C、D位置是怎样的,并请画出示意图?小圆盘共自转了几圈?
有一个电动玩具,它有一个8.28×5.14的长方形盘(单位:厘米)和一个半径为1厘米的小圆盘(盘中画有娃娃脸)它们的连接点为A、B(如图)如果小圆盘沿着长方形内壁,从A点出发,不停的滚动(无滑动),最后回到原来位置,请你计算一下,小圆盘(娃娃脸)在B、C、D位置是怎样的,并请画出示意图?小圆盘共自转了几圈?