题目内容
【题目】用小棒按照如下方式摆图形。
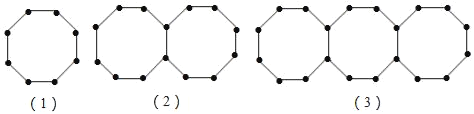
(1)摆1个八边形需要8根小棒,摆2个八边形需要_____根小棒,摆3个八边形需要_____根小棒,摆30个八边形需要_____根小棒。
(2)如果想摆n个八边形,需要_____根小棒。
(3)有2010根小棒,可以摆_____个这样的八边形。
【答案】15 22 211 1+7n 287
【解析】
(1)(2)由图可以看出:
摆一个八边形需要8根小棒,摆2个八边形需要8+7=15根小棒以后每增加一个八边形,摆3个八边形需要8+2×7=22根小棒,也就是每增加一个八边形就增加7根小棒,所以摆n个八边形需要8+(n-1)×7=1+7n根小棒,据此即可解答。
(3)由摆一个八边形需要8根小棒可得:1+7n=2010,解得n即可。
(1)根据题干分析可得:
摆成n个八边形就需要1+7n根小棒,
当n=2时,需要小棒1+2×7=15(根),
当n=3时,需要小棒1+3×7=22(根),
当n=30时,需要小棒1+30×7=211(根),
所以,摆2个八边形需要15根小棒,摆3个八边形需要22根小棒,摆30个八边形需要211根小棒。
(2)由(1)可知:摆n个八边形,需要1+7n根小棒
(3)1+7n=2010
1+7n-1=2010﹣1
7n=2009
7n÷7=2009÷7
n=287
所以,有2010根小棒,可以摆287个这样的八边形。
故答案为:15;22;211,1+7n;287。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目