题目内容
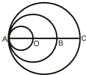如图中，AO=OB=CB，最小圆与最大圆的面积比是________．
1：9
分析：因为AO=OB=CB，可知最小圆与最大圆的直径比是1：3，进而得知最小圆与最大圆的半径比是1：3，把最小圆的半径看做“1”，则最大圆的半径就为3，利用公式分别求出最小圆与最大圆的面积，进而求出它们的比即可．
解答：因为AO=OB=CB，
所以最小圆与最大圆的半径的比是1：3，
最小圆的面积：π×12=π，
最大圆的面积：π×32=9π，
最小圆与最大圆的面积比：π：9π=1：9；
故答案为：1：9．
点评：解决此题关键是根据题意推出最小圆与最大圆的半径的比，进而利用公式：圆的面积=圆周率×半径2，分别求出面积，进而求出面积比即可．
分析：因为AO=OB=CB，可知最小圆与最大圆的直径比是1：3，进而得知最小圆与最大圆的半径比是1：3，把最小圆的半径看做“1”，则最大圆的半径就为3，利用公式分别求出最小圆与最大圆的面积，进而求出它们的比即可．
解答：因为AO=OB=CB，
所以最小圆与最大圆的半径的比是1：3，
最小圆的面积：π×12=π，
最大圆的面积：π×32=9π，
最小圆与最大圆的面积比：π：9π=1：9；
故答案为：1：9．
点评：解决此题关键是根据题意推出最小圆与最大圆的半径的比，进而利用公式：圆的面积=圆周率×半径2，分别求出面积，进而求出面积比即可．
练习册系列答案
相关题目
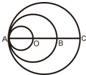如图中，AO=OB=CB，最小圆与最大圆的面积比是