题目内容
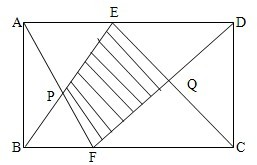如右图所示，在长方形ABCD中，三角形ABP的面积为20平方厘米，三角形CDQ的面积为35平方厘米．求阴影四边形的面积．分析：由题意可知：S△ABF+S△CDF=S△BCE，等式的两边分别去掉公共部分，即S△BFP+S△FCQ，则剩余的部分的面积仍然相等，即S△ABP+S△CDQ=S四边形FQEP（阴影部分），据此代入数据即可求解．
解答：解：因为S△ABF+S△CDF=S△BCE，
等式的两边分别去掉公共部分，即S△BFP+S△FCQ，
则剩余的部分的面积仍然相等，
即S△ABP+S△CDQ=S四边形FQEP（阴影部分），
所以阴影部分的面积为=20+35=55（平方厘米）；
答：阴影四边形的面积是55平方厘米．
等式的两边分别去掉公共部分，即S△BFP+S△FCQ，
则剩余的部分的面积仍然相等，
即S△ABP+S△CDQ=S四边形FQEP（阴影部分），
所以阴影部分的面积为=20+35=55（平方厘米）；
答：阴影四边形的面积是55平方厘米．
点评：解答此题的主要依据是：三角形的面积是与其等底等高的平行四边形面积的一半．
练习册系列答案
相关题目
（2010?保靖县）如图所示，在相距10厘米的两条平行线d和c之间，有正方形A和长方形B．正方形A沿直线d以每秒2厘米的速度向右运动，长方形B固定不动，A和B两个图形有重叠部分的时间持续多少秒？（单位：厘米）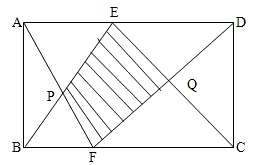
如右图所示，在长方形ABCD中，三角形ABP的面积为20平方厘米，三角形CDQ的面积为35平方厘米．求阴影四边形的面积．