题目内容
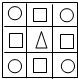
有很多白色或黑色的棱长是1厘米的小正方体.取其中的27个,拼成一个棱长是3厘米的大正方体,每个面都各用2个黑色的小正方体拼成相同的图案,见例图.例图中正方体的每一个面的图案相同,用8个或9个黑色的小正方体就可以拼成例图中的大正方体.除例图之外,还可以用27块小正方体拼成每面是其它图案的大正方体,且大正方体六个面的图案相同.请回答:
(1)拼成的大正方体的每一个面的图案,有可能是下面①-⑦图的那些图形?
(2)在上一问中可以按要求拼成的大正方体各用了几个黑色的小正方体?

(1)拼成的大正方体的每一个面的图案,有可能是下面①-⑦图的那些图形?
(2)在上一问中可以按要求拼成的大正方体各用了几个黑色的小正方体?

分析:根据每个小正方体在大正方体的表面露出面的个数多少,可以把组成大正方体的27个小正方体分成四类,第一类是在大正方体的顶点处的小正方体,有8个,每个露出3个面;第二类是在大正方体的棱长上的小正方体,有12个,每个露出2个面;第三类是在大正方体的面上的小正方体,有6个,每个露出1个面;第四类是在大正方体的中心的小正方体,有1个,露出0个面;根据小正方体在大正方体一个表面中露出的图案位置,可以把大正方体一个面中露出9个小正方体的面分成三类第一类是圆形所在的位置是大正方体的顶点,如果在这个位置出现阴影,在其他两个面中必定同时出现阴影;第二类是正方形所在的位置是在大正方体的棱长上,如果这个位置出现阴影,另一个表面中对应的位置也会出现阴影;第三类是三角形所在的位置是在大正方体的表面上,只出现一次阴影,据此进行分析即可解答.

解答:解:如图表示大正方体的六个面,黑色五角星表示是黑色正方体的表面,
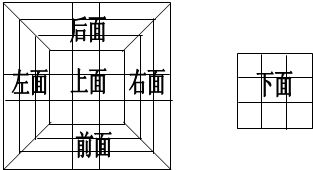
情况1:如图,左面和下面的图案已经符合图形1的要求,但是后面的另一个黑色阴影只能在白色五角星所在的两个位置,由左面和下面来看这两个位置又都不是黑色的小正方体,相矛盾,所以大正方体的六个面不可能都是图2中的图案;
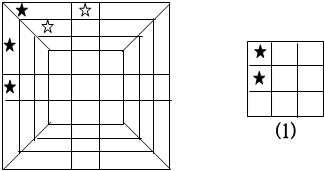
情况2:如图,在下面和左面,都已经符合要求,前面的另一个阴影只能是表示五角星所在的两个位置,相矛盾,所以大正方体的六个面不可能都是图2中的图案;
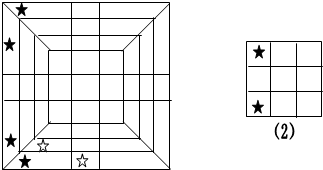
情况3:如图,大正方体的表面可以是图3,这种情况下是用了5个黑色小正方体拼成:
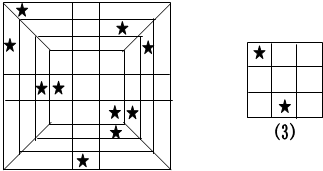
情况4:人大正方体的表面可以是图形4,这种情况下,是用了4个黑色小正方体拼组成的:
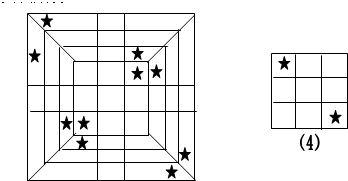
情况5:如图,大正方体的表面可以是图形5,这种情况下是用了9个黑色小正方体拼组成的:

情况6:如图,大正方体的表面可以图形6,这种情况下是用了6个黑色小正方体组成的:

情况7:如图,上下、前后四个面的图案都符合图形7的要求,但是左右两个面的黑色阴影无论放在哪个位置,都影响原来四个面中的情况,所以大正方体的6个面不可能是图形7的情况.


情况1:如图,左面和下面的图案已经符合图形1的要求,但是后面的另一个黑色阴影只能在白色五角星所在的两个位置,由左面和下面来看这两个位置又都不是黑色的小正方体,相矛盾,所以大正方体的六个面不可能都是图2中的图案;

情况2:如图,在下面和左面,都已经符合要求,前面的另一个阴影只能是表示五角星所在的两个位置,相矛盾,所以大正方体的六个面不可能都是图2中的图案;

情况3:如图,大正方体的表面可以是图3,这种情况下是用了5个黑色小正方体拼成:

情况4:人大正方体的表面可以是图形4,这种情况下,是用了4个黑色小正方体拼组成的:

情况5:如图,大正方体的表面可以是图形5,这种情况下是用了9个黑色小正方体拼组成的:

情况6:如图,大正方体的表面可以图形6,这种情况下是用了6个黑色小正方体组成的:

情况7:如图,上下、前后四个面的图案都符合图形7的要求,但是左右两个面的黑色阴影无论放在哪个位置,都影响原来四个面中的情况,所以大正方体的6个面不可能是图形7的情况.

点评:此题主要考查立方体的表面染色问题,明确正方体顶点处的小正方体3面涂色,棱长上的小正方体两面涂色,面上的小正方体一面涂色,是解决本题的关键,再利用平面图形画出涂色小正方体的位置,即可分析解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目