Question

六（2）班有56个学生，在一次测验中，答对第一题的34人，答对第二题的29人，两题都答对的15人．那么，两题都不对的有（　　）人．

A．7

B．8

C．12

D．20

Answer 1

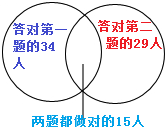
分析：根据题干：答对第一题的34人，答对第二题的29人，两题都答对的15人．由此只要求出答对第一题或是第二题或者两题都答对的人数（即至少答对一题的人数）之和，那么剩下的就是两题都不对的人数，由此可以画图分析：所以可得至少答对一题的人数为：34+29-15=48（人），由此即可求得两题都不对的人数．

解答：解：根据题干分析可得：
56-（34+29-15），
=56-48，
=8（人）；
答：两题都不对的有8人．
故选：B．

点评：此题考查了利用容斥原理解决实际问题的方法的灵活应用，利用画图法分析更简洁明了，此题的关键是先求出至少一题答对的人数．