题目内容
同一底上的两个角相等的梯形一定是等腰梯形．
√
√
．（判断对错）分析：过点B作BE∥AD，根据已知可得到四边形ABED是平行四边形，从而得到AD=BE，又因为BE∥AD，∠D=∠C，从而可得到BE=BC=AD，从而推出梯形ABCD是等腰梯形．
解答：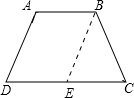
解：过点B作BE∥AD，
因为AB∥DC，BE∥AD，
所以四边形ABED是平行四边形．
所以AD=BE．
因为ABBE∥AD，
所以∠D=∠BEC．
因为AB∠D=∠C，
所以∠BEC=∠C．
所以BE=BC．
所以BC=AD．
所以梯形ABCD是等腰梯形．
所以上面的说法是正确的．
故答案为：√．
解：过点B作BE∥AD，因为AB∥DC，BE∥AD，
所以四边形ABED是平行四边形．
所以AD=BE．
因为ABBE∥AD，
所以∠D=∠BEC．
因为AB∠D=∠C，
所以∠BEC=∠C．
所以BE=BC．
所以BC=AD．
所以梯形ABCD是等腰梯形．
所以上面的说法是正确的．
故答案为：√．
点评：本题主要考查了对等腰梯形的判定．
练习册系列答案
名校课堂系列答案
相关题目