题目内容
有两个周长相等而面积不等的长方形.甲的长和宽分别是80米和50米.如果两个长方形的长和宽都分别增加10米,这时乙长方形的面积增加
1400
1400
平方米.分析:如图所示,由题意可知:乙长方形的长+宽=甲长方形的长+宽,设乙长方形的长是x,宽是y,长和宽都增加10米后,和原来长方形比较增加了一个边长为10的正方形和两个长方形,这三部分面积之和=10x+10y+10×10=10(x+y)+100=10×(80+50)+100=1400,据此解答即可.
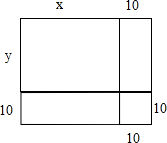

解答:解:因为乙长方形的长+宽=甲长方形的长+宽,即x+y=80+50,
设乙长方形的长是x,宽是y,
长和宽都增加10米后,和原来长方形比较增加了一个边长为10的正方形和两个长方形,
这三部分面积之和=10x+10y+10×10,
=10(x+y)+100,
=10×(80+50)+100,
=1400(平方米);
答:这时乙长方形的面积增加1400平方米.
故答案为:1400.
设乙长方形的长是x,宽是y,
长和宽都增加10米后,和原来长方形比较增加了一个边长为10的正方形和两个长方形,
这三部分面积之和=10x+10y+10×10,
=10(x+y)+100,
=10×(80+50)+100,
=1400(平方米);
答:这时乙长方形的面积增加1400平方米.
故答案为:1400.
点评:此题主要考查长方形的周长和面积的计算方法的灵活应用,关键是先求出长方形的长和宽的值.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目