题目内容
下面图形中,( )不可以密铺.
A、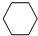 | B、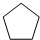 | C、 | D、 |
分析:平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠; (3)连续铺成一片. 能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°或每个内角都能整除360°,并使相等的边互相重合.正五边形就不具备这样的特点.
解答:解:正六边形,正方形、正三角形每个内角能整除360°,都可以密铺;
正五边形每个内角是[(5-2)×180°-360°]÷5=108°,不能整除360°,所以不能密铺.
故选:B.
正五边形每个内角是[(5-2)×180°-360°]÷5=108°,不能整除360°,所以不能密铺.
故选:B.
点评:考查了平面镶嵌(密铺)问题,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角或一个图形的每个内角都是360的因数.

练习册系列答案
相关题目
下面图形中,( )对称轴最少.
| A、正方形 | B、等边三角形 | C、圆 |
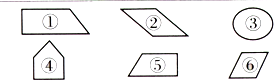 下面图形中,( )和( )是平行四边形.
下面图形中,( )和( )是平行四边形.| A、①④ | B、②⑤ | C、③⑥ | D、②⑥ |