Question

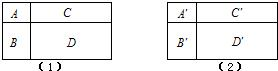
一个周长是56厘米的大长方形，按图中（1）与（2）所示意那样，划分为四个小长方形．在（1）中小长方形面积的比是：A：B=1：2，B：C=1：2．而在（2）中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3．求大长方形的面积．

Answer 1

分析：要求大长方形的面积，需求出它的长和宽，由条件“在（1）中小长方形面积的比是：A：B=1：2，B：C=1：2．而在（2）中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3”可知：D的宽是大长方形宽的

2

3

，D^′的宽是大长方形宽的

3

4

，D的长是

4

5

×（28-大长方形的宽），D^′的长是

9

10

×（28-大长方形的宽），由此便可以列式计算．

解答：解：设大长方形的宽为x，则长为28-x
因为D的宽=

2

3

x，D^′的宽=

3

4

x，所以，D^′的宽-D的宽=

x

12

．
D长=

4

5

×（28-x），D^′长=

9

10

×（28-x），
D^′长-D长=

1

10

×（28-x），
由题设可知　

x

12

：

28-x

10

=

1

3

即

28-x

10

=

x

4

，于是

28

10

=

7x

20

，x=8．
于是，大长方形的长=28-8=20，从而大长方形的面积为8×20=160平方厘米．
答：大长方形的面积是160平方米．

点评：此题比较复杂，主要考查比的关系，应利用比的意义，找清数量见的比，再利用题目条件，就可以进行计算求得结果．