题目内容
4.算式$\frac{9}{10}$+$\frac{99}{100}$+$\frac{999}{1000}$+…+$\frac{999999}{1000000}$结果的整数部分是5.分析 根据上式加数的特点,分别差0.1,0.01,0.001,0.0001…0.000001就等于1,所以假设都等于1,所以算式的结果是6,再用10减去0.1,0.01,0.001…0.000001的和,所以最后的结果是6-0.111111,计算后可得到答案.
解答 解:$\frac{9}{10}$+$\frac{99}{100}$+$\frac{999}{1000}$+…+$\frac{999999}{1000000}$
=(1+1+1+1+1+1)-(0.1+0.01+0.01+…+0.000001)
=6-0.111111
=5.888889
答:算式$\frac{9}{10}$+$\frac{99}{100}$+$\frac{999}{1000}$+…+$\frac{999999}{1000000}$结果的整数部分是5.
故答案为:5.
点评 解答此题的关键是使用凑数法,然后再在和里减去多加上的数即可.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
14.若有理数a在数轴上对应的点如图所示,则a,-a,-1的大小关系是( )


| A. | a<-a<-1 | B. | -a<a<-1 | C. | -a<-1<a | D. | a<-1<-a |
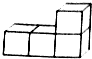 如图,由四个小正方形组成的几何体中,若每个小正方体的棱长都是1,则从上面看到的该几何体的形状图的面积是3.
如图,由四个小正方形组成的几何体中,若每个小正方体的棱长都是1,则从上面看到的该几何体的形状图的面积是3. ,图中有3条线段,6条射线.
,图中有3条线段,6条射线.