题目内容
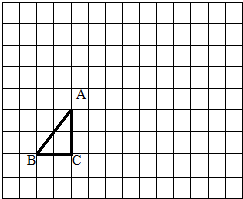
如图，在长方形ABCD中，AB=6厘米，BC=8厘米，四边形EFHG的面积是3平方厘米，阴影部分的面积和是________平方厘米．
15
分析：由题意可知：因为S△BDC=S△BEC，所以S△DGC=S△BEG同理，S△ABF=S△FCE，因此S阴=S△BEC-S△HBC+S四边形EFHG，从而问题得解．
解答：平行四边形面积为6×8=48（平方厘米），
三角形BEC面积为48÷2=24（平方厘米），
三角形BHC面积为48÷4=12（平方厘米）．
因为S△BDC=S△BEC，
所以S△DGC=S△BEG同理，S△ABF=S△FCE，
因此S阴=S△BEC-S△HBC+S四边形EFHG，
=24-12+3，
=15（平方厘米）；
答：阴影部分的面积和是15平方厘米．
故答案为：15．
点评：解决此题的关键是利用等积转换，即等底等高的三角形面积相等，将阴影部分重组，从而利用已知条件求得阴影部分的面积．
分析：由题意可知：因为S△BDC=S△BEC，所以S△DGC=S△BEG同理，S△ABF=S△FCE，因此S阴=S△BEC-S△HBC+S四边形EFHG，从而问题得解．
解答：平行四边形面积为6×8=48（平方厘米），
三角形BEC面积为48÷2=24（平方厘米），
三角形BHC面积为48÷4=12（平方厘米）．
因为S△BDC=S△BEC，
所以S△DGC=S△BEG同理，S△ABF=S△FCE，
因此S阴=S△BEC-S△HBC+S四边形EFHG，
=24-12+3，
=15（平方厘米）；
答：阴影部分的面积和是15平方厘米．
故答案为：15．
点评：解决此题的关键是利用等积转换，即等底等高的三角形面积相等，将阴影部分重组，从而利用已知条件求得阴影部分的面积．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
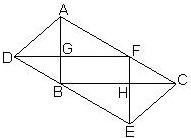两个形状和大小都一样的直角三角形△ABC和△DEF，如图放置，它们的面积都是2003平方厘米，而每一个三角形的顶点恰好都落在另一个三角形的斜边上．这两个直角三角形的重叠部分是一个长方形，那么四边形ADEC的面积为
（2008?宝应县）（1）如表每小方格面积1平方厘米，先在图中画一个长4cm，宽3cm的长方形，再在长方形中画一个最大的圆，求出圆的面积．
（1）如表每小方格面积1平方厘米，先在图中画一个长4cm，宽3cm的长方形，再在长方形中画一个最大的圆，求出圆的面积．