题目内容
大人们遇到了下面的问题，你能帮助进行正确的估算吗？请直接列出估算算式，并写出结果．
如：信息技术老师为学校去买电脑，每台电脑3980元，买5台大约需要多少元？
4000×5≈20000（元）
①后勤张阿姨带1000元给幼儿园买苹果，每箱苹果95元，张阿姨最多能买多少箱苹果？
②李爷爷的果园里有91棵苹果树．收获时，他先摘完3棵树，共装满5筐，每筐约重38千克．估计一下，李爷爷的果园大约共可收获苹果多少千克？
如：信息技术老师为学校去买电脑，每台电脑3980元，买5台大约需要多少元？
4000×5≈20000（元）
①后勤张阿姨带1000元给幼儿园买苹果，每箱苹果95元，张阿姨最多能买多少箱苹果？
②李爷爷的果园里有91棵苹果树．收获时，他先摘完3棵树，共装满5筐，每筐约重38千克．估计一下，李爷爷的果园大约共可收获苹果多少千克？
分析：①把95元看成100元，然后用总钱数除以单价就是可以，买的箱数；
②先把91棵数，看成90棵数，求出90棵有多少个3棵，没3棵可以装5箱，由此求出一共可以装多少箱；然后把每箱38千克看成40千克，用总箱数乘每箱的重量即可．
②先把91棵数，看成90棵数，求出90棵有多少个3棵，没3棵可以装5箱，由此求出一共可以装多少箱；然后把每箱38千克看成40千克，用总箱数乘每箱的重量即可．
解答：解：①1000÷95≈1000÷100=10（箱）；
答：张阿姨最多能买10箱苹果．
②91÷3≈30；
30×5×38，
≈30×5×40，
=150×40，
=6000（千克）；
答：李爷爷的果园大约共可收获苹果6000千克．
答：张阿姨最多能买10箱苹果．
②91÷3≈30；
30×5×38，
≈30×5×40，
=150×40，
=6000（千克）；
答：李爷爷的果园大约共可收获苹果6000千克．
点评：本题考查了估算的实际应用，分析题干列出算式，把接近整十、整百的数看成整十、整百进行估算．
练习册系列答案
名校课堂系列答案
相关题目
表示其中的第n项，那么
。
及
。又如向日葵花序中小花或籽粒的排列，顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
)，34∶55(
)，89∶144(
)，在一些大型样本中，这个比值甚至为144∶233(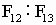
)。同样，生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数，一般总是落在斐波那契数列3，5，8和13相邻的两数中。
表示其中的第n项，那么
。
及
。又如向日葵花序中小花或籽粒的排列，顺时针螺旋数与逆时针螺旋数之比一般是12∶21(
)，34∶55(
)，89∶144(
)，在一些大型样本中，这个比值甚至为144∶233(
)。同样，生物学家研究了各种菠萝球形花的鳞片顺、逆时针的螺旋数，一般总是落在斐波那契数列3，5，8和13相邻的两数中。