Question

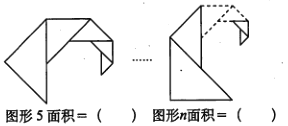
【题目】如下图，下面一系列图形中第一个最小的等腰直角三角形的面积都是1，后一个等腰直角三角形的斜边恰好是前一个等腰直角三角形的直角边的2倍，请计算每个图形的面积，并填在相应的空中。

Answer 1

【答案】1 3 7 15 31 2n－1

【解析】本题考查的是数形结合的规律。认真观察、比较、归纳每组图形与第一个图形的关系是本题的关键。

根据题意，已知第一个图形的面积是1，要求每个图形的面积，我们不妨找出每个图形与第一个图形的关系，通过分割将每个图形分割成若干个第一个图形，如下图所示。

由图示可知，第一个图形的面积是1；

第二个图形中有3个第一个图形，即面积是3；

第三个图形中有7个第一个图形，即面积是7；

第四个图形中有15个第一个图形，即面积是15；

观察归纳数列1、3、7、15、……的规律，可得1＝21－1；3＝22－1；7＝23－1；15＝24－1，所以下一个数是25－1＝31，第n个数是2n－1，故第5个图形的面积是31，第n个图形的面积是2n－1。